Predictions from Best-Fit Lines

1. Making Predictions From Best-Fit Lines

A best-fit line can be used to make predictions about the response variable based on some value of the explanatory variable.

EXAMPLE

The data here is the miles and airfares for different city destinations from the Minneapolis/Saint Paul Airport.

Destination	Miles	Airfare
Boston	1,266	263
Charleston	1,294	306
Chicago	407	128
Denver	834	212
Detroit	611	261

In this case, you'd figure that miles is the explanatory variable because, in theory, things that are further away should cost more to get to, based on gasoline, etc.

The regression equation is predicted airfare is equal to 113.11 plus 0.137 times miles.



Suppose you are asking what the predicted airfare would be for a flight from Atlanta from Minneapolis, which would have a total distance of 1,064 miles. To find the airfare, simply put 1,064 in for miles in the regression equation.



The airfare would be about $259. The biggest question here, though, is how confident are you in that prediction? How confident are you that your prediction is close to what it actually costs to get to Atlanta from Minneapolis?

Look back at the data.

Destination	Miles	Airfare
Boston	1,266	263
Charleston	1,294	306
Chicago	407	128
Denver	834	212
Detroit	611	261

This linear model is based on data that had distances that were less than the distance to Atlanta and also more than the distance to Atlanta. It seems to make sense to use this model to predict what the cost would be for a place that is 1,064 miles from Minneapolis.

EXAMPLE

What about the predicted airfare for a flight to Anchorage at a distance of 3,163 miles from Minneapolis?



The predicted airfare from Anchorage to Minneapolis is $546.44, however, the actual airfare is $727.48. In this case, the prediction differs largely from what the actual airfare ends up being. So why are these values so far apart?

You can't really use the prediction equation to predict what the airfare to Anchorage would be because this distance is so far out of the bounds of the data that you use to actually create the model.

The range of miles that was used to create your model was from about 400 miles away from Minneapolis to about 1,300 miles away from Minneapolis. Charleston was the longest distance away, and Chicago was the shortest distance away. What you're saying is that within the window of 400 to about 1,300, the line gives reasonable predictions for airfare.

Destination	Miles	Airfare
Boston	1,266	263
Charleston	1,294	306
Chicago	407	128
Denver	834	212
Detroit	611	261

Outside of that window, though, it might not. Therefore, you have to be very cautious about using this prediction line to predict the airfare to Milwaukee, which is closer than 400 miles to Minneapolis, or to a place like Anchorage. It might not give accurate predictions outside of this particular window.

2. Extrapolation

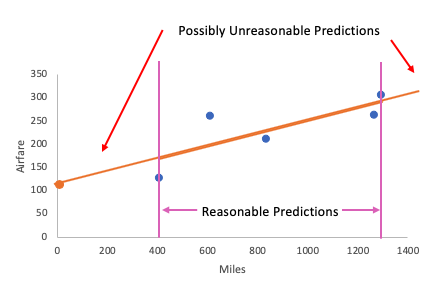
The whole idea of making predictions outside of a range is called extrapolation. It's using the linear model to make predictions outside the range of values for which the estimate was intended.

It's not always bad to extrapolate, because sometimes linear trends do continue outside of the window from the data that made them, but not always.

However, proceed with caution if you do end up extrapolating data because it is risky. You're trusting the linear model to continue outside of the bounds that created the model itself. Using the linear model to try and predict outside those bounds might be an unwise decision.

EXAMPLE

Men's Olympic gold medal 100-meter dash times have decreased at a rate of about 100th of a second per year for the last 60 years. The graph below shows this relationship.

Someone who extrapolates might say that if this trend continues, then in about 1,000 years, there will be a person whose gold medal sprint time is zero seconds.

Clearly, this is nonsense. You can't use this line to predict what might happen even 100 years down the road, much less 1,000 years down the road. Extrapolation might not be a good idea, especially with this particular data set, because it can lead to nonsense results.

term to know

Extrapolation

Using the regression line to make predictions outside the window for which the model was intended.