Table of Contents |
A best-fit line can be used to make predictions about the response variable based on some value of the explanatory variable.
EXAMPLE
The data here is the miles and airfares for different city destinations from the Minneapolis/Saint Paul Airport.| Destination | Miles | Airfare |
|---|---|---|
| Boston | 1,266 | 263 |
| Charleston | 1,294 | 306 |
| Chicago | 407 | 128 |
| Denver | 834 | 212 |
| Detroit | 611 | 261 |


| Destination | Miles | Airfare |
|---|---|---|
| Boston | 1,266 | 263 |
| Charleston | 1,294 | 306 |
| Chicago | 407 | 128 |
| Denver | 834 | 212 |
| Detroit | 611 | 261 |
EXAMPLE
What about the predicted airfare for a flight to Anchorage at a distance of 3,163 miles from Minneapolis?
| Destination | Miles | Airfare | |
|---|---|---|---|
| Boston | 1,266 | 263 | |
| Charleston | 1,294 | 306 | |
| Chicago | 407 | 128 | |
| Denver | 834 | 212 | |
| Detroit | 611 | 261 | |
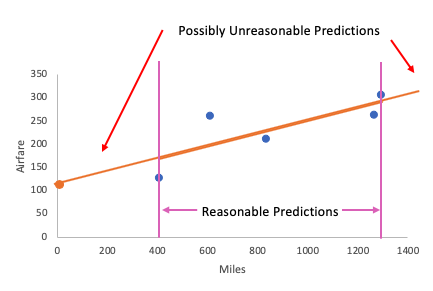
| |||
The whole idea of making predictions outside of a range is called extrapolation. It's using the linear model to make predictions outside the range of values for which the estimate was intended.
It's not always bad to extrapolate, because sometimes linear trends do continue outside of the window from the data that made them, but not always.
However, proceed with caution if you do end up extrapolating data because it is risky. You're trusting the linear model to continue outside of the bounds that created the model itself. Using the linear model to try and predict outside those bounds might be an unwise decision.
EXAMPLE
Men's Olympic gold medal 100-meter dash times have decreased at a rate of about 100th of a second per year for the last 60 years. The graph below shows this relationship.
Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.