Table of Contents |
A quadratic expression is a polynomial that can be written in the form shown below.

A specific type of quadratic expression is called the difference of squares.
EXAMPLE
You know that the expression shown here is a quadratic expression because the highest exponent in the expression is 2.

This is called a difference of squares expression, because there are two values squared, x and the integer, with subtraction between the two.
Difference of squares expressions can be factored similarly to other quadratic expressions.
EXAMPLE
Suppose you want to factor the difference of squares expression from the example above.
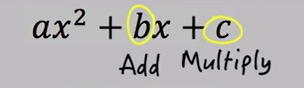



Therefore, in general, you can factor the difference of squares equations as shown here.


Source: This work is adapted from Sophia author Colleen Atakpu.