Table of Contents |
An inequality is a statement that two quantities are not equal to each other. In general, we see statements that use inequality symbols to show that one quantity is greater than or less than another. However, inequality symbols can be strict or non-strict. The distinction here is that non-strict inequalities "allow" the two quantities to be exactly equal to each other, while strict inequality symbols do not. This is the difference between "greater than" (>) and "greater than or equal to" (≥), for example.
It is also important to remember that when graphing inequalities and when plotting solutions on a number line, we use open circles, curved braces, and dotted lines for strict inequalities; and we use closed circles, square brackets, and solid lines for non-strict inequalities.
When we find solutions to a quadratic inequality, we are looking for all x-values that make the inequality statement true. Let's take a look at an example.
EXAMPLE
Consider this quadratic inequality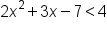 .
.
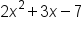 less than 4, and there is a set of x-values that makes
less than 4, and there is a set of x-values that makes 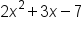 greater than or equal to 4. The former is the solution set to the inequality, since it makes our statement true, while the latter is the set of all non-solutions because it makes the inequality statement false.
greater than or equal to 4. The former is the solution set to the inequality, since it makes our statement true, while the latter is the set of all non-solutions because it makes the inequality statement false.
To find solutions to a quadratic inequality, it is often helpful to first think of the relationship as an equation, and then consider the inequality once solutions to the equation have been found. This is because we have a variety of tools at our disposal to solve quadratic equations, such as factoring, completing the square, or using the quadratic formula.
We generally follow these steps to solve a quadratic inequality.
In other words, when we treat the inequality as an equation and find solutions to the equation, we identify critical points to define the solution region. We then choose any value we want within certain intervals (defined by these critical points) and see if they yield true or false statements to the original inequality.
EXAMPLE
Find the solutions for the quadratic inequality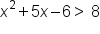 .
.
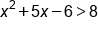
|
Rewrite as an equation set equal to zero |
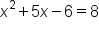
|
Subtract 8 from both sides |
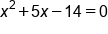
|
Factor the equation |
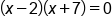
|
Set each factor equal to zero |

|
Evaluate |

|
Solutions to the equation |
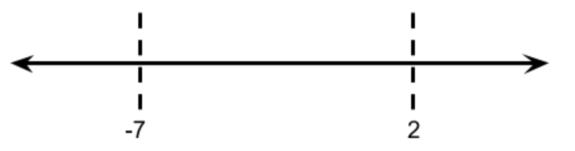
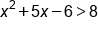 as
as 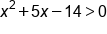 .
.
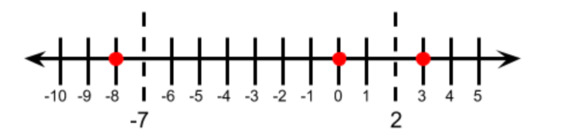
| x |
|
Result | Interval |
|---|---|---|---|
| -8 |
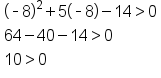
|
This inequality is TRUE, so this interval is part of the solution. |

|
| 0 |

|
This inequality is NOT TRUE, so this interval is NOT part of the solution. |
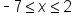
|
| 4 |
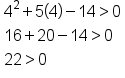
|
This inequality is TRUE, so this interval is part of the solution. |
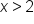
|
 and
and 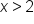 are included in the solution region, while the values
are included in the solution region, while the values 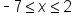 make up the non-solution region. Note that we used less than or greater than symbols with our solutions. This is because the original inequality
make up the non-solution region. Note that we used less than or greater than symbols with our solutions. This is because the original inequality 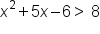 was a strict inequality, meaning that these points are not part of the inequality. We can write the solution to the inequality as:
was a strict inequality, meaning that these points are not part of the inequality. We can write the solution to the inequality as:
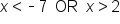
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License