Rational Equations Representing Work and Rate

1. The Relationship between Work, Rate, and Time

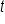We can express the relationship between work, rate, and time using the equation , where is work, is rate, and is time.

If it takes x number of hours to complete a job, we can describe the rate as (1 job) / (x hours), or as the rational expression , with the unit being jobs per hour.

When two people work together, the total work is the sum of their individual work. We will use these relationships to answer some questions involving work, rate, and time.

---

2. Solving a Work, Rate, and Time Problem For an Individual

Abby and Bobby are maintenance workers for a building management company. They share the task of mowing the lawn and trimming the hedges at the different complexes the company manages.

If Abby were to work alone, it would take 30 minutes for her to complete the work at one building. If her coworker Bobby helps, they can complete the same amount of work in only 18 minutes.

How long would it take Bobby to complete the work by himself?

To model this scenario, we can create a work, rate, and time chart that organizes known and unknown information. Our chart will have columns for Work, Rate, and Time, and rows for Abby and Bobby:

	Rate	Time	Work
Abby
Bobby

We know information about the rate of Abby's work if she works alone, as well as the time it takes for Abby and Bobby to complete the work together. Abby can complete the work in 30 minutes so we will describe Abby's rate as 1 job per 30 minutes. We don't know how long it takes Bobby to complete one job by himself, so we will use the variable x to describe the number of minutes it takes him to complete a job by himself, and say that his rate is 1 job per x minutes.

We can also enter 18 minutes in the time column for both Abby and Bobby to show that if they work together, they can complete a job in 18 minutes:

	Rate	Time	Work
Abby		18 min.
Bobby		18 min.

Recall that , so if we multiply their rate by time, we can get the proportion of one job that they complete on their own in 18 minutes:

	Rate	Time	Work
Abby		18 min.
Bobby		18 min.

Abby's work is 1 job over 30 minutes times 18 minutes and that equals 18 over 30 job, which simplifies to 3/5 job. Notice how the units of minutes cancel, which confirms that our units for work is jobs.

For Bobby, we used the rate 1 job over x minutes, and then multiply it by 18 minutes to show the proportion of work Bobby can do in 18 minutes.

Using the fact that when two people work together, their total work (1 job) is the sum of their individual work, we have the rational equation:

To solve this equation, one strategy is to rewrite every term so that it has a common denominator. If all terms have a common denominator, then we can create an equation with just the numerators, which makes our equation easier to solve. Also, since all the terms are in terms of jobs, we can simply write the equation as and solve for x:

	Create common denominators by multiplying factors in both numerator and denominator
	Evaluate multiplication
	Create an equation with only numerators
	Subtract 3x from both sides
	Divide by 2
	Our solution

This means that if Bobby were to work alone, it would take him 45 minutes to complete one job.

---

3. Solving a Work, Rate, and Time Problem For Combined Rates

Andrew and Amanda are cleaning the windows in their house. Andrew can clean the windows in 3 hours. Amanda can clean the windows in 2 hours.

How long will it take to clean the windows together?

We can set up another work, rate, and time chart. In the chart, we have Andrew and Amanda, and we're looking at their rate, time, and work completed.

	Rate	Time	Work
Andrew
Amanda

We know that Andrew can complete the job of cleaning the windows in 3 hours, so we can say his rate is . For the same task, it takes Amanda 2 hours, so we can say her rate is .

	Rate	Time	Work
Andrew
Amanda

We don't know how long it will take for them to clean the windows together so we can put x hours in for time. Work is rate times time, so we can multiply Andrew's and Ashley's rates by x time to find their portion of work.

	Rate	Time	Work
Andrew		x hours
Amanda		x hours

Work is rate times time. For Andrew, his work is going to be equal to 1 job over 3 hours times x hours, which is equal to x over 3 job. For Amanda, her expression for work will be 1 job over 2 hours times x hours, which is equal to x over 2 job.

Now we can create a rational equation by adding Andrew's work and Amanda's work.

The work is 1 job of cleaning the windows in the house, so their combined work is equal to 1. In the rational equation, x is the amount of time it takes Andrew and Amanda to clean the windows together. Since all the terms are in terms of jobs, we can simply write the equation as .

With rational equations, we can add them together once they have common denominators. Once we have this, we can solve for x using the expressions in the numerator.

	Create common denominators by multiplying factors in both numerator and denominator
	Evaluate multiplication
	Create an equation with only numerators
	Combine like terms
	Divide by 5
	Our solution

If Andrew and Amanda work together, they can clean the windows in 1.2 hours.