Real Number Types

1. Real Number Types

There are a variety of different number types that make up our real number system. Numbers such as -2, 7.8, and pi can be categorized into different groups within the set of all real numbers. Real numbers are numbers that can be expressed as a decimal and placed on the number line.

We are going to illustrate different types of real numbers using the picture below:

We can refer to this image as representing the universe of all real numbers. Everything that fits within this picture means that it exists within the universe of real numbers. The first type of real number we are going to talk about is natural numbers.

term to know

Real Numbers

Numbers that can be an expression as a decimal and placed on the number line.

1a. Natural Numbers

Natural numbers are numbers used in counting, not including zero: {1, 2, 3.... }. Adding natural numbers to our diagram, we see that it is included in our set of real numbers:

Notice that natural numbers do not include zero, since zero represents the absence of a quantity (something we cannot physically count). If we included zero along with all of our natural numbers, this would be the set of all whole numbers.

1b. Whole Numbers

Whole numbers would be: {0, 1, 2, 3, ....}. Let's show whole numbers on our diagram:

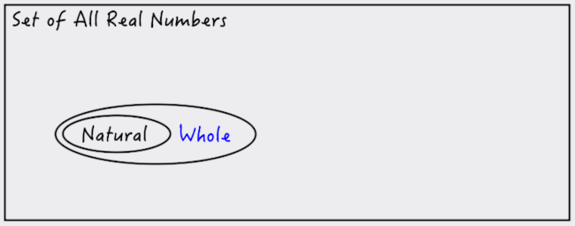
As you can see, every natural number can also be called a whole number. The only difference between whole numbers and natural numbers is that zero is a whole number, but it's not a natural number.

1c. Integers

So far, all of our numbers have been non-negative (positive natural numbers, and then zero). Including negative numbers brings us to what we refer to as integers, which come up all the time in math. Integers are natural numbers and their opposites, including zero.

So by opposites, we mean "negative." So while natural numbers are {1, 2, 3... }, integers are {-3, -2, -1, 0, 1, 2, 3...}. Notice that zero is also an integer. Let's include integers on our picture:

Notice that all natural numbers are integers, and all whole numbers are integers, but not all integers are whole numbers or natural numbers (because whole and natural numbers do not include any negative numbers).

term to know

Integers

Natural numbers and their opposites, including zero.

1d. Rational Numbers

Next, we get into two very special types of numbers, the first being rational numbers. Looking at the word "rational" we see "ratio." A rational number is a ratio of two integers.

In other words, a rational number is a fraction. But not any fraction, the numerator and denominator have to be integers. This means no decimal numbers, like 2.5 (that's not an integer). Also note that since this is a fraction, there is one integer that b cannot be: zero. We can't divide by zero, so as long as b ≠ 0, a and b can be any integer to form a rational number.

Let's place rational numbers on our diagram:

Notice that the pattern still continues: all natural, whole, and integer numbers are also considered rational numbers (but not the other way around).

term to know

Rational Numbers

Numbers which can be expressed as a ratio of two integers, a/b.

1e. Irrational Numbers

There is one other type of real number that we would like to include on our picture, and it breaks the pattern we have built up so far. This number type is called irrational numbers, and a simple way to think about irrational numbers is that they are not rational, or in other words, cannot be represented as a ratio of integers.

Because irrationals cannot be expressed as a ratio of integers, irrational numbers cannot be considered natural, whole, or integer numbers. What does this look like in our picture?

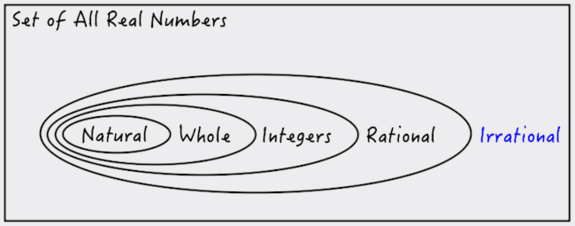
Irrational numbers still exist within our set of real numbers, but they do not enclose natural, whole, integer, and rational numbers.

term to know

Irrational Numbers

Numbers which cannot be represented as a ratio of integers.

2. Characteristics of Rational and Irrational Numbers

Next, let's talk about the characteristics of rational and irrational numbers. Think about how to express as a decimal number. This is equivalent to 0.375. Notice that our decimal number eventually ends. We call this a terminating decimal pattern. The decimal digits stop at a point (aside from implied zeros that go on forever).

What about the rational number 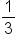? As a decimal, this is 0.33333... The digit 3 goes on forever and ever. But we know this is a rational number. So rational numbers either have a terminating decimal pattern or a repeating decimal pattern.

big idea

Rational numbers are characterized by either terminating or repeating decimal patterns, such as 0.375 or 0.3333...

Now let's look at the decimal patterns of irrational numbers. Pi (π) is a common irrational number. Notice that we use a special symbol for this number. Pi is approximately 3.14159. This is only an approximation of pi because the decimal pattern never stops, and there is no recognizable decimal pattern. So a characteristic of an irrational number is that the decimal pattern does not terminate (keeps going forever and ever), and it does not repeat (there is no repeating decimal pattern). Many square roots are also irrational, such as the square root of 3 which equals approximately 1.7320508.

big idea

Irrational numbers are characterized by a non-terminating decimal pattern and a non-repeating decimal pattern. For example, pi can be expressed as 3.141592654.... but it contains an infinite number of decimals, with no recognizable pattern of digits.

hint

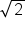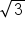Not all square roots are irrational. , , and 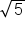are (look at their decimal pattern), but what about square roots such as or 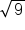? These evaluate to integers (because they are perfect squares), and integers are rational numbers.