This lesson discusses identifying skewness with measures of center. By the end of the lesson, you should be able to identify the relationship between mean, median, and mode on a skewed distribution, and be able to use these measures of center to identify skew. Specifically, this lesson covers:
1. Measures of Center and Skew
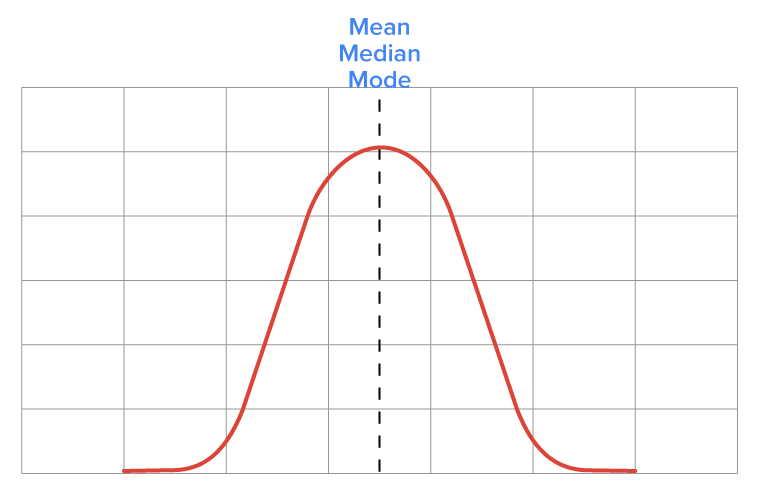
What can measures of center tell us about the skew of data? Look at this graph, which shows a normal distribution. It’s symmetrical. The mean, median, and mode are identical. Therefore, for data with little or no skew, all three measures of center will be equal.
-
For a normal distribution, mean = median = mode. This will also be roughly true for real data with little or no skew.
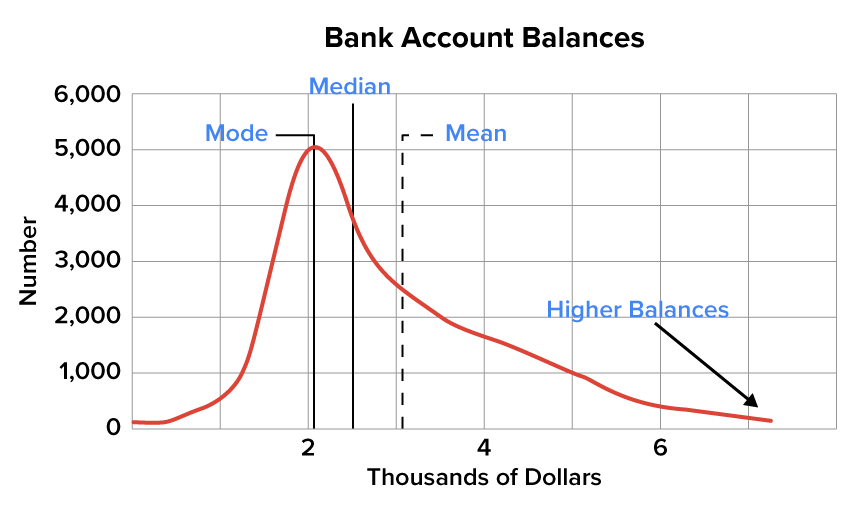
Bank account balances are an example of a right-skewed distribution. A few people have quite a bit of money in their bank account, but many more don’t. In this situation, the mode and the median are going to be relatively low, and the mean is going to be higher. That’s simply because a small number of large balances pull up the mean.
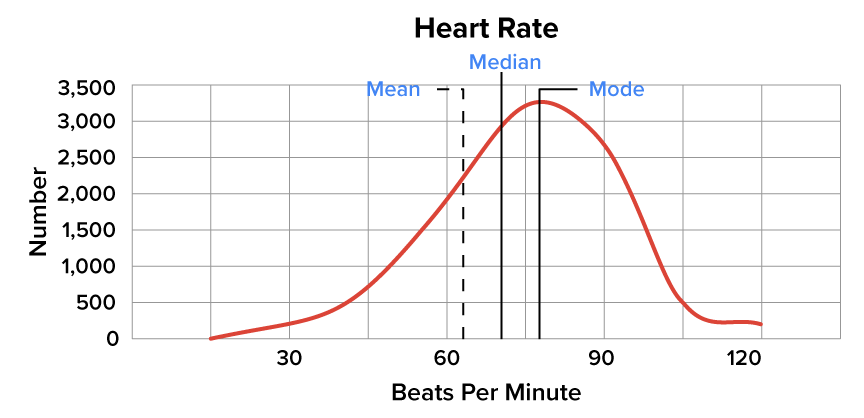
For an example of a left-skewed distribution, look at the heart rate of a sample of people. You’re going to see the heart rate measured in beats per minute, and the mean beats per minute is probably somewhere around the 70 or 80 mark. You will see some beats that are higher or lower than that. However, there will be relatively few people with a low heart rate. That’s going to bring you to a situation reflected by a left-skewed distribution.
IN CONTEXT
When Bill Gates (or choose your favorite billionaire) sits at a cafe, the average (mean) customer instantly becomes a billionaire!
This case illustrates how the mean can be very misleading. In the case of the mean, a few extreme observations (outliers) can have a big effect. The median and the mode, however, would change very little.
2. Identifying Skew Using Measures of Center
-
How can you tell if a distribution is going to be skewed one way or the other?
You can look at a graph, but you can also look at the mean, median, and mode.
- If the mean is greater than the median and the mode, it is a right-skewed distribution.
- If the mean is equal to the median and the mode, it’s a normal distribution.
- If the mean is less than the median and the mode, it is a left-skewed distribution.
|
Situation
|
Skew
|
|
Mean > Median
|
Right
|
|
Mean > Mode
|
Right
|
|
Mean = Median
|
Normal
|
|
Mean = Mode
|
Normal
|
|
Mean < Median
|
Left
|
|
Mean < Mode
|
Left
|
-
What type of skew would you expect from the following data sets?
-
Life span (age at death) for people in a developed countryA small number of people might live short lives due to illness or accident, but with good healthcare, most can expect to live into their 60s or 70s, and very few would live past 100. In this case, the mean would be reduced by outliers with shorter lives, but the median would change less (mean < median). This data would be left-skewed.
-
Commute times for workers in your cityIn the United States, most workers live less than 30 miles from work, but a few may commute a longer distance. In this case, the mean would be increased by those with relatively longer commutes, but the median and mode would be less affected (mean > median and mode). This data would be right-skewed.
In this lesson, you learned that symmetrical distributions have roughly equal values for mean, median, and mode. You learned to identify skewed data with measures of center. Considering the relationship between measures of center and skew, right-skewed data has a mean that is larger than the median and mode, and left-skewed data has a mean that is smaller than the median and mode.


