Table of Contents |
In the previous lesson, we learned how to graph inequalities, but how could we write a specific interval without showing a picture on the number line? We need a few more symbols to express whether the endpoint is included within the interval or not. These include square brackets and parentheses.
| Symbols for Notating Intervals | |
| Endpoint is Included in Interval | Endpoint is Not Included in Iinterval |
|---|---|
| [ or ] | ( or ) |

|

|
When writing an inequality using interval notation, square brackets correspond to the closed circles on the number line. They indicate that the endpoint is included in the interval. The parentheses or rounded brackets are used when there are open circles on the number line, and the endpoint is not included in the interval.
EXAMPLE
Write the highlighted range on the number line in interval notation.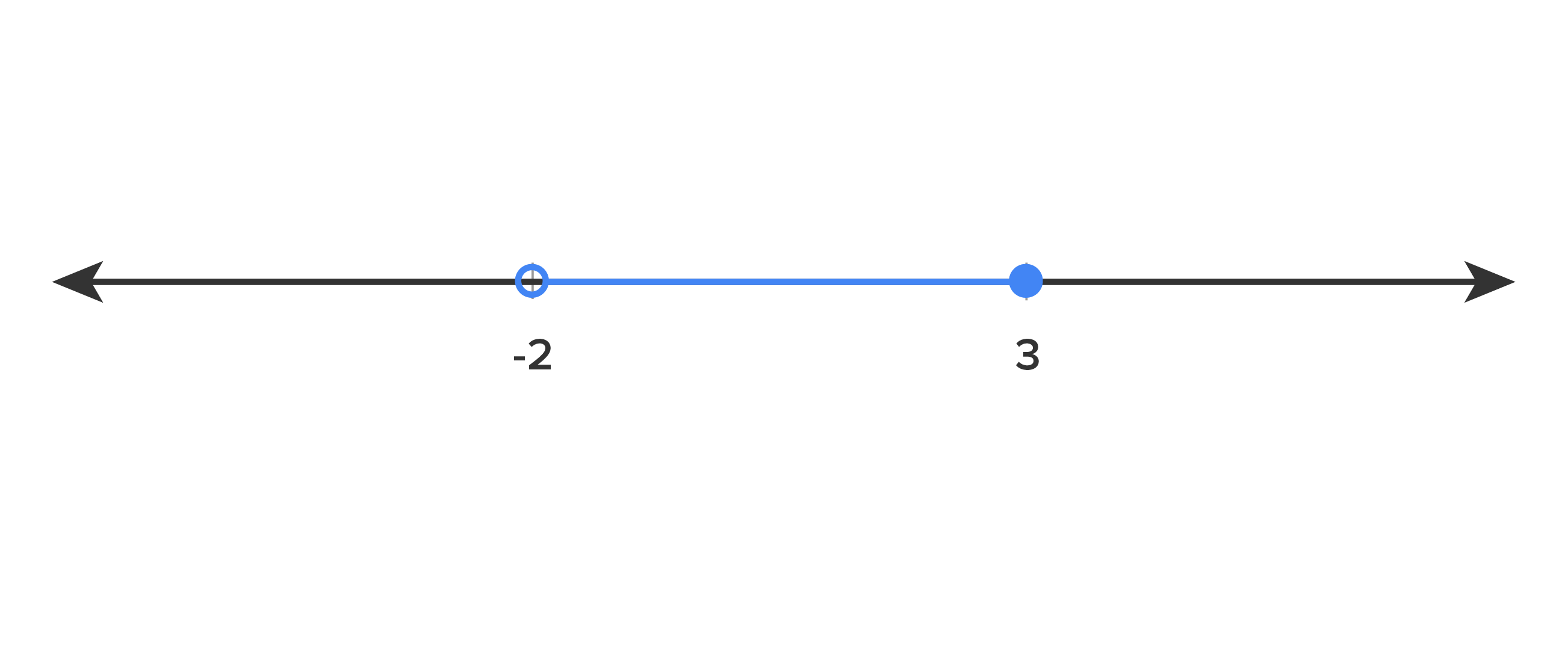
EXAMPLE
Write the highlighted range on the number line in interval notation.
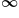 . If the arrow is pointing in the positive direction, this is
. If the arrow is pointing in the positive direction, this is 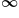 (positive infinity). If the arrow is pointing in the negative direction, this is
(positive infinity). If the arrow is pointing in the negative direction, this is 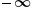 (negative infinity). Numbers can get bigger and bigger, but we will never actually reach
(negative infinity). Numbers can get bigger and bigger, but we will never actually reach 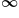 . So,
. So, 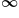 is an endpoint of the interval, but is not included in the interval. Therefore, we will always use a parenthesis with positive or negative infinity.
is an endpoint of the interval, but is not included in the interval. Therefore, we will always use a parenthesis with positive or negative infinity.
 .
The next endpoint is positive infinity, which is written as
.
The next endpoint is positive infinity, which is written as  with a parenthesis.
with a parenthesis.
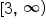 .
.
When looking at number lines with a range of highlighted values, we can write the range of values in a couple of different ways: in a format called set notation, and in interval notation. We will use inequalities to help us write the intervals in set notation. Let’s look at the symbols so far and add in the inequality symbols also.
| Endpoint Symbols for Notating Intervals | |
| Endpoint is Included in Interval | Endpoint is Not Included in Interval |
|---|---|

|

|
| [ or ] | ( or ) |
 or or 
|
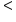 or or 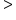
|
If we add inequalities to the chart of endpoint symbols, we see that the less than (<) and the greater than (>) symbols indicate that the endpoint is not included in the interval. We see that the less than or equal to (≤) or greater than or equal to (≥) symbols do include the endpoints in the interval. If we have an expression such as  greater than or equal to −2, this means our variable can be any number greater than or equal to −2, such as 5, 0, −1, −1.9999, or even −2.
greater than or equal to −2, this means our variable can be any number greater than or equal to −2, such as 5, 0, −1, −1.9999, or even −2.
In set notation, we can use inequalities to help us write the interval in set notation. In set notation, we define the range of values as a set of numbers, and we use curly brackets to define the set, with a description of what is to be included in the set.
EXAMPLE
Write the highlighted range in set notation.
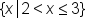 . This reads as “all x-values, such that x is greater than (but not including) -2, but x is also less than and can include 3.”
. This reads as “all x-values, such that x is greater than (but not including) -2, but x is also less than and can include 3.”
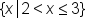 .
.
EXAMPLE
Write the highlighted range in set notation.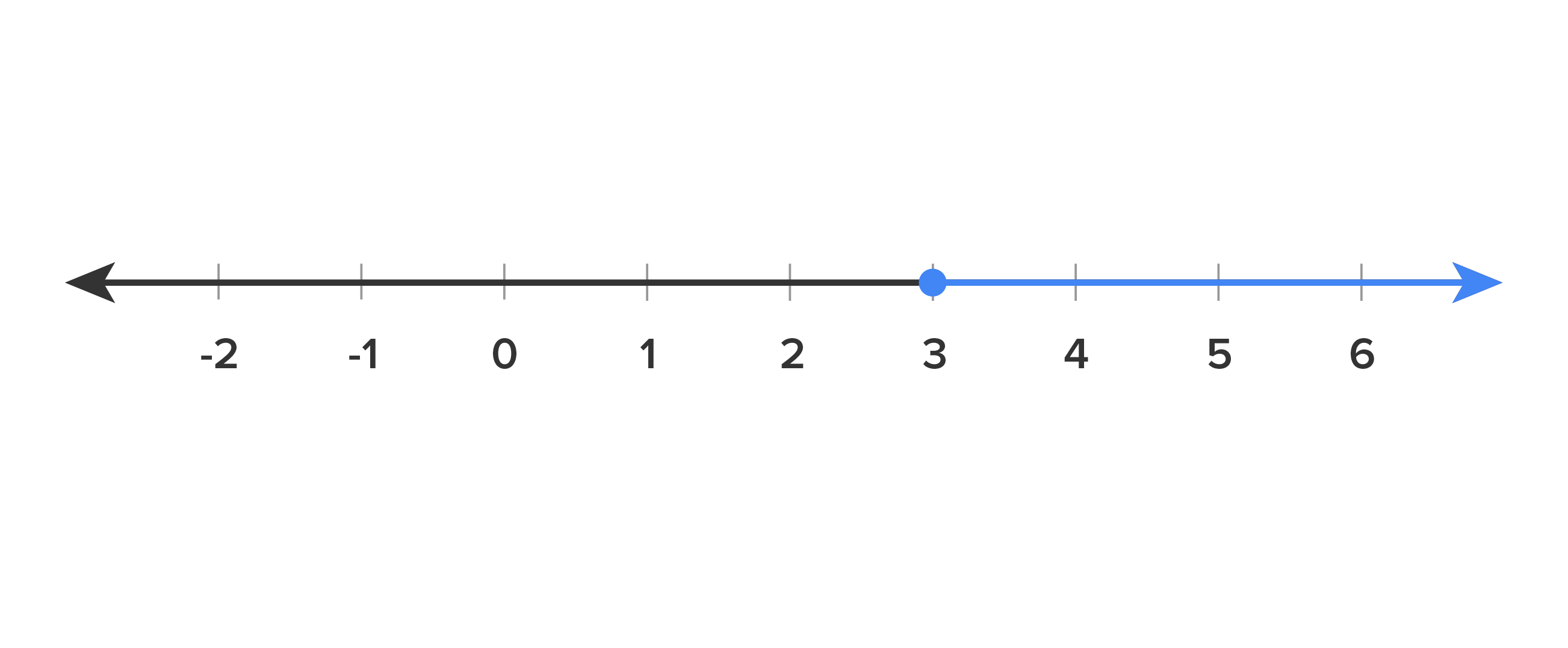
 . This is read as, "all x-values, such that x is greater than or equal to 3.” So, that means that x can be any number in the highlighted range that is greater than or equal to 3.
. This is read as, "all x-values, such that x is greater than or equal to 3.” So, that means that x can be any number in the highlighted range that is greater than or equal to 3.
 .
.
Let's practice writing in set and interval notation, using number line solutions.
EXAMPLE
Examine the number line below:
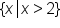 . Note that our inequality symbol does not include the exact value of 2.
. Note that our inequality symbol does not include the exact value of 2.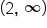 . Note that we use a parenthesis to the left of 2, and also a parenthesis to the right of infinity.
. Note that we use a parenthesis to the left of 2, and also a parenthesis to the right of infinity.Let's look at a more complicated example:
EXAMPLE
Examine the number line below: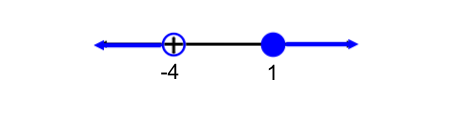
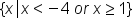 . We use the connecting word "or" because values that fit within either inequality statement will fit the number line solution.
. We use the connecting word "or" because values that fit within either inequality statement will fit the number line solution.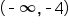 . and the second interval is
. and the second interval is  . To accept both intervals as solutions for x, we use the symbol for union, U, to connect the two intervals. To complete our solution in interval notation, we have
. To accept both intervals as solutions for x, we use the symbol for union, U, to connect the two intervals. To complete our solution in interval notation, we have  .
.Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License