Before we begin, you should first understand what is meant by statistical significance. When you calculate a test statistic in a hypothesis test, you can calculate the p-value. The p-value is the probability that you would have obtained a statistic as large (or small, or extreme) as the one you got if the null hypothesis is true. It's a conditional probability.
Sometimes you’re willing to attribute whatever difference you found between your statistic and your parameter to chance. If this is the case, you fail to reject the null hypothesis, if you’re willing to write off the differences between your statistic and your hypothesized parameter.
If you’re not, meaning it's just too far away from the mean to attribute to chance, then you’re going to reject the null hypothesis in favor of the alternative.
This is what it might look like for a two-tailed test.
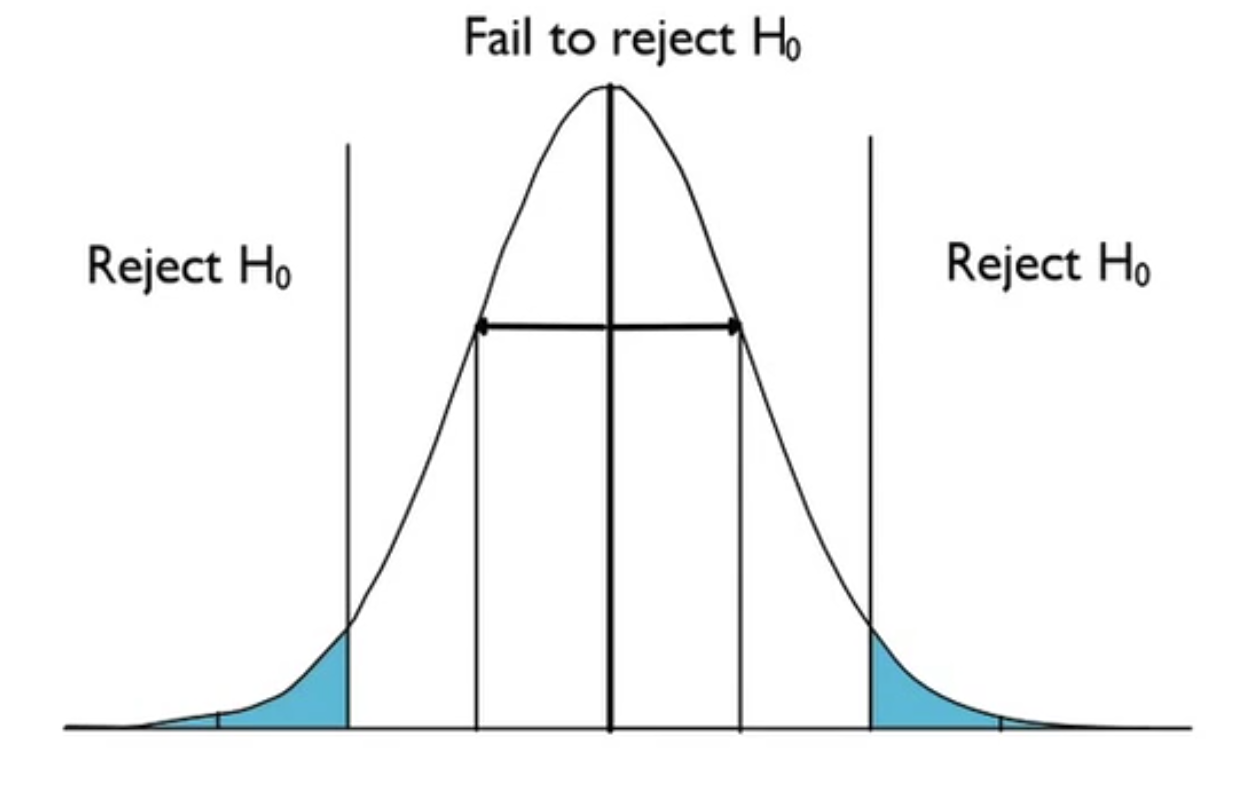
The hypothesized mean is right in the center of the normal distribution. Anything that is considered to be too far away--something like two standard deviations or more away--you would reject the null hypothesis. Anything you might attribute to chance, within the two standard deviations, you would fail to reject the null hypothesis. Again, this is assuming that the null hypothesis is true.
However, think about this. All of this curve assumes that the null hypothesis is true, but you make a decision to reject the null hypothesis anyway if the statistic you got is far away. It means that this would rarely happen by chance. But, it's still the wrong thing to do technically, if the null hypothesis is true. This idea that we're comfortable making some error sometimes is called a significance level.
The probability of rejecting the null hypothesis in error, in other words, rejecting the null hypothesis when it is, in fact, true, is called a Type I Error.
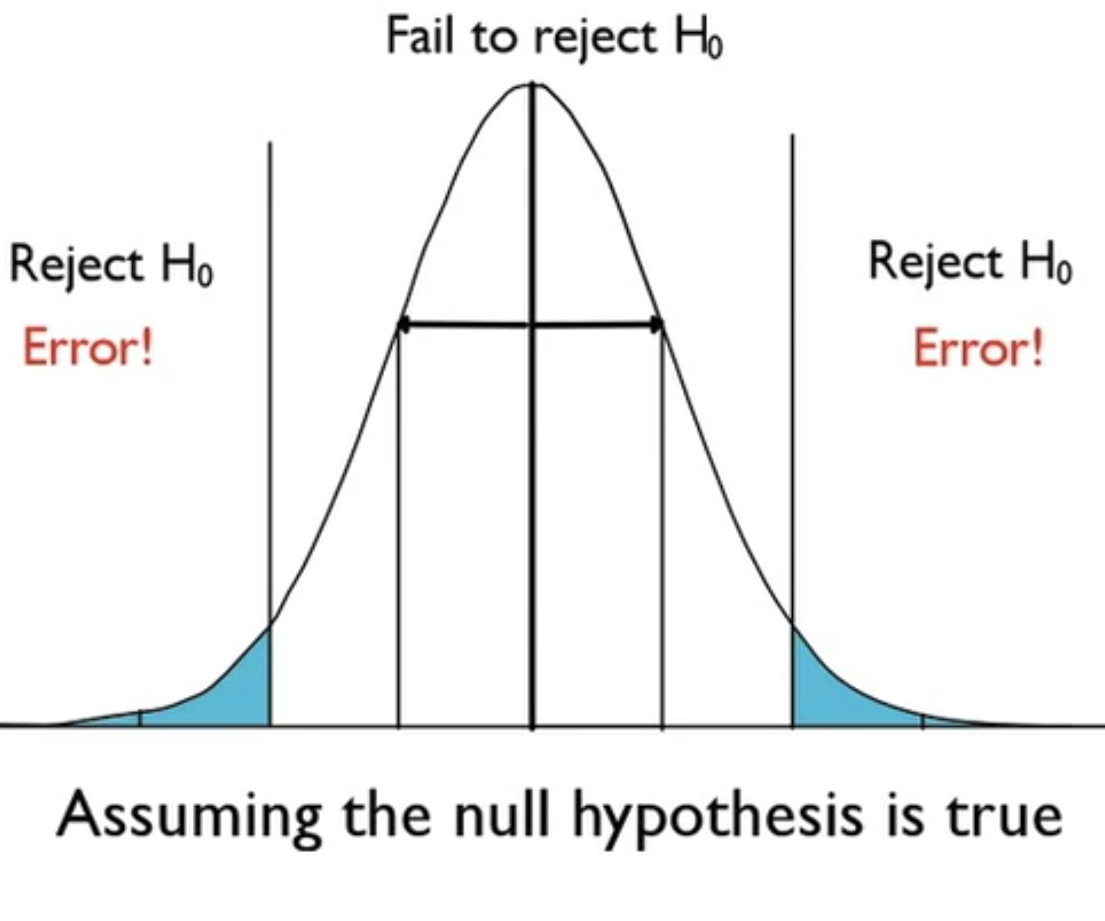
Fortunately, you get to choose how big you want this error to be. You could have stated that three standard deviations from the mean on either side as "too far away". Or, for instance, you could say you only want to be wrong 1% of the time, or 5% of the time, meaning that you are rejecting the null hypothesis in error that often.
This value is known as the significance level. It is the probability of making a Type I error. We denote it with the Greek letter alpha (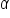 ).
).
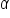 .
.
When you choose how big you want alpha to be, you do it before you start the tests. You do it this way to reduce bias because if you already ran the tests, you could choose an alpha level that would automatically make your result seem more significant than it is. You don't want to bias your results that way.
Take a look back at this visual here.
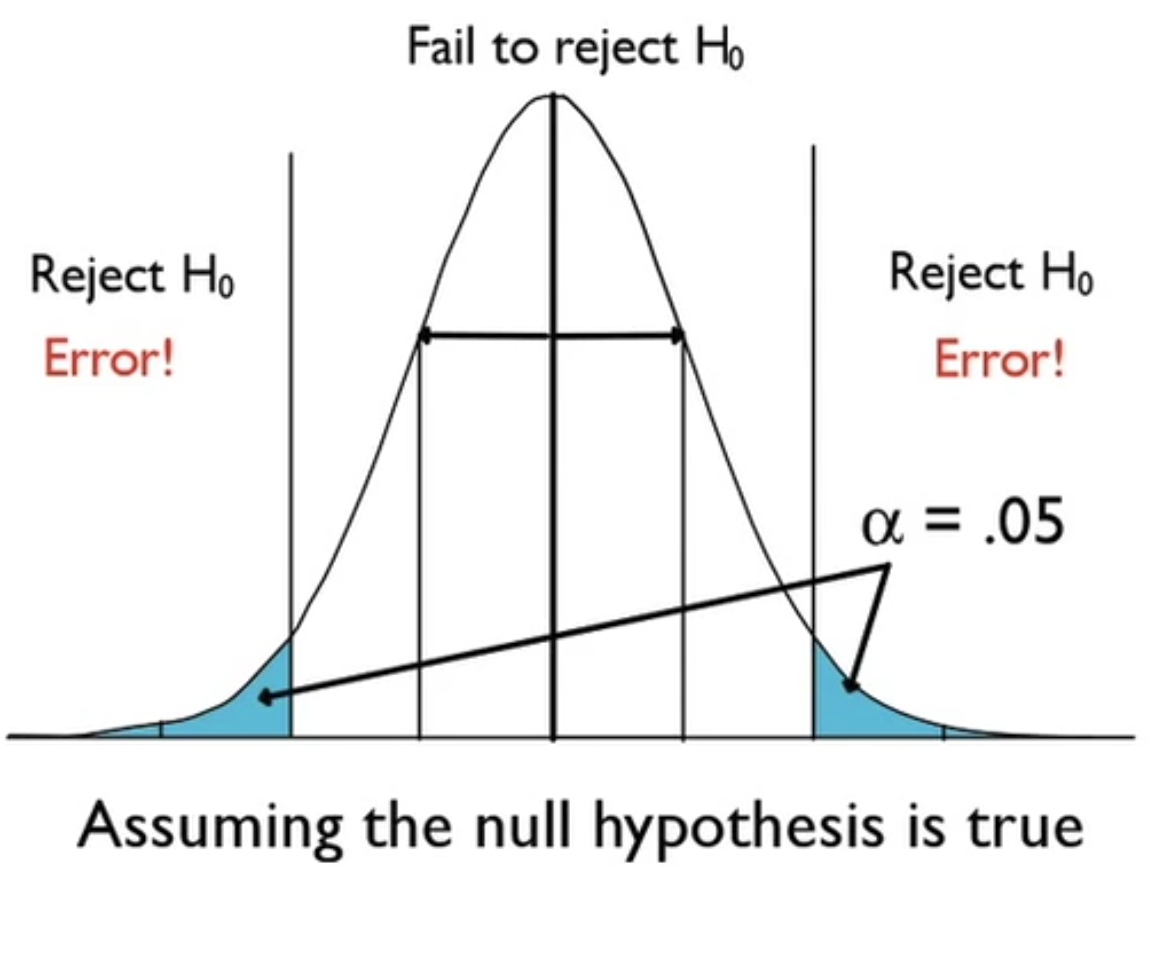
The alpha, in this case, is 0.05. If you recall, the 68-95-99.7 rule says that 95% of the values will fall within two standard deviations of the mean, meaning that 5% of the values will fall outside of those two standard deviations. Your decision to reject the null hypothesis will be 5% of the time; the most extreme 5% of cases, you will not be willing to attribute to chance variation from the hypothesized mean.
The level of significance will also depend on the type of experiment that you're doing.
EXAMPLE
Suppose you are trying to bring a drug to market. You want to be extremely cautious about how often you reject the null hypothesis. You will reject the null hypothesis if you’re fairly certain that the drug will work. You don't want to reject the null hypothesis of the drug not working in error, thereby giving the public a drug that doesn't work.If you want to be really cautious and not reject the null hypothesis in error very much, you'll choose a low significance level, like 0.01. This means that only the most extreme 1% of cases will have the null hypothesis rejected.
If you don't believe a Type I Error is going to be that bad, you might allow the significance level to be something higher, like 0.05 or 0.10. Those still seem like low numbers. However, think about what that means. This means that one out of every 20, or one out of every ten samples of that particular size will have the null hypothesis rejected even when it's true. Are you willing to make that mistake one out of every 20 times or once every ten times? Or are you only willing to make that mistake one out of every 100 times? Setting this value to something really low reduces the probability that you make that error.
It is important to note that you don't want the significance level to be too low. The problem with setting it really low is that as you lower the value of a Type 1 Error, you actually increase the probability of a Type II Error.
A Type II Error is failing to reject the null hypothesis when a difference does exist. This reduces the power or the sensitivity of your significance test, meaning that you will not be able to detect very real differences from the null hypothesis when they actually exist if your alpha level is set too low.
You might wonder, what is power? Power is the ability of a hypothesis test to detect a difference that is present.
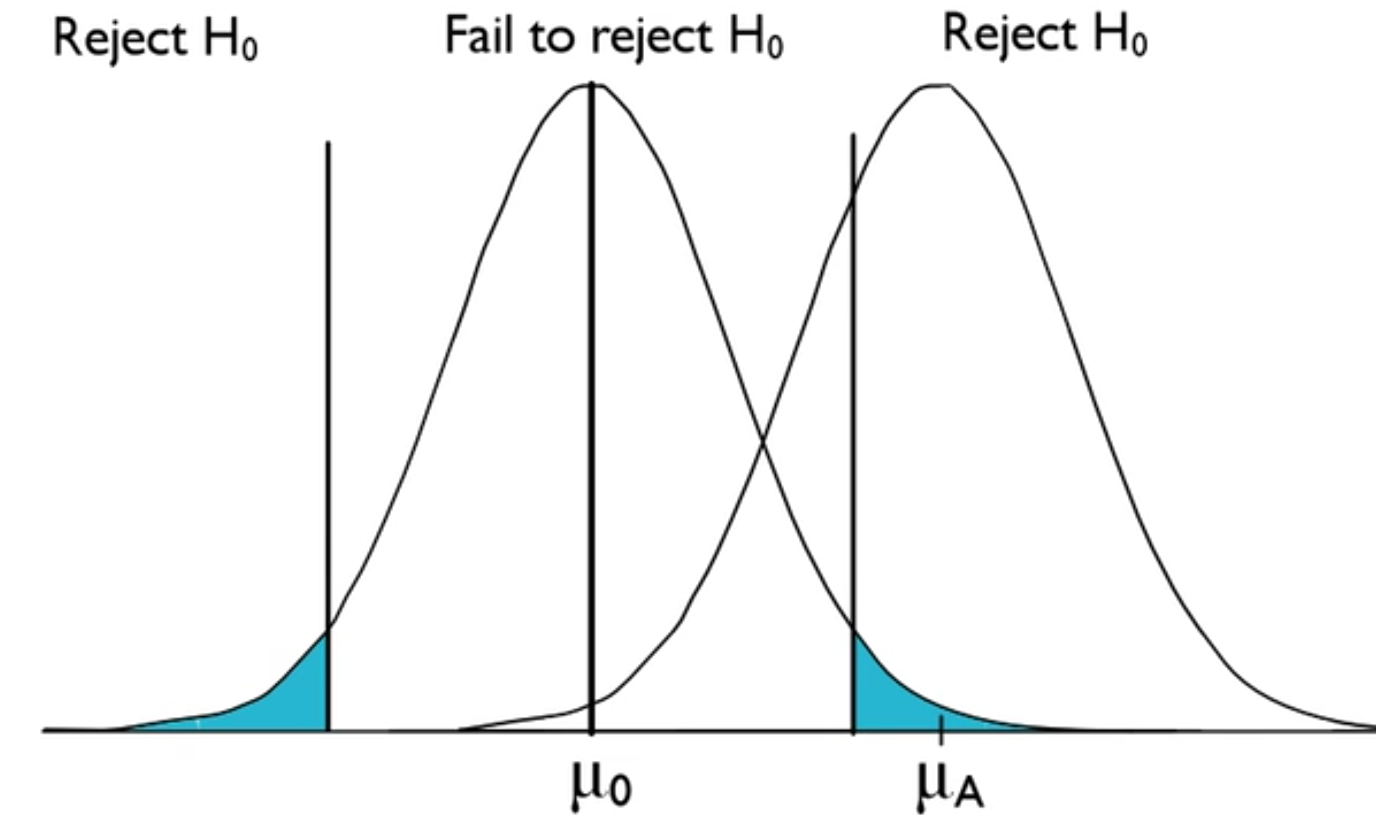
Consider the curves below. Note that μ0 is the hypothesized mean and μA is the actual mean. The actual mean is different than the null hypothesis; therefore, you should reject the null hypothesis. What you end up with is an identical curve to the original normal curve.
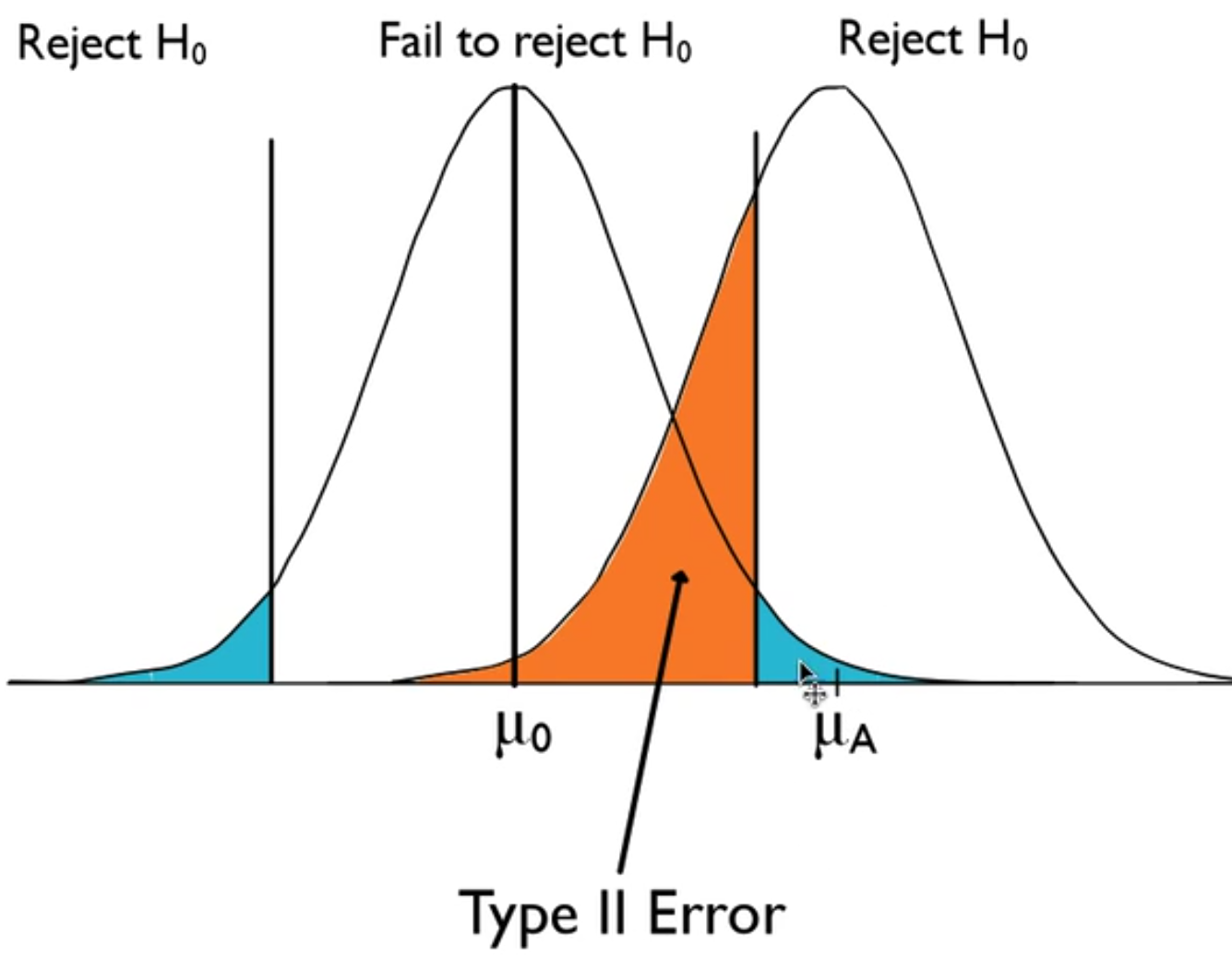
If you take a look at the curve below, it illustrates the way the data is actually behaving, versus the way you thought it should behave based on the null hypothesis. This line in the sand still exists, which means that because we should reject the null hypothesis, this area in orange is a mistake.
Failing to reject the null hypothesis is wrong, if this is actually the mean, which is different from the null hypothesis' mean. This is a type II error.
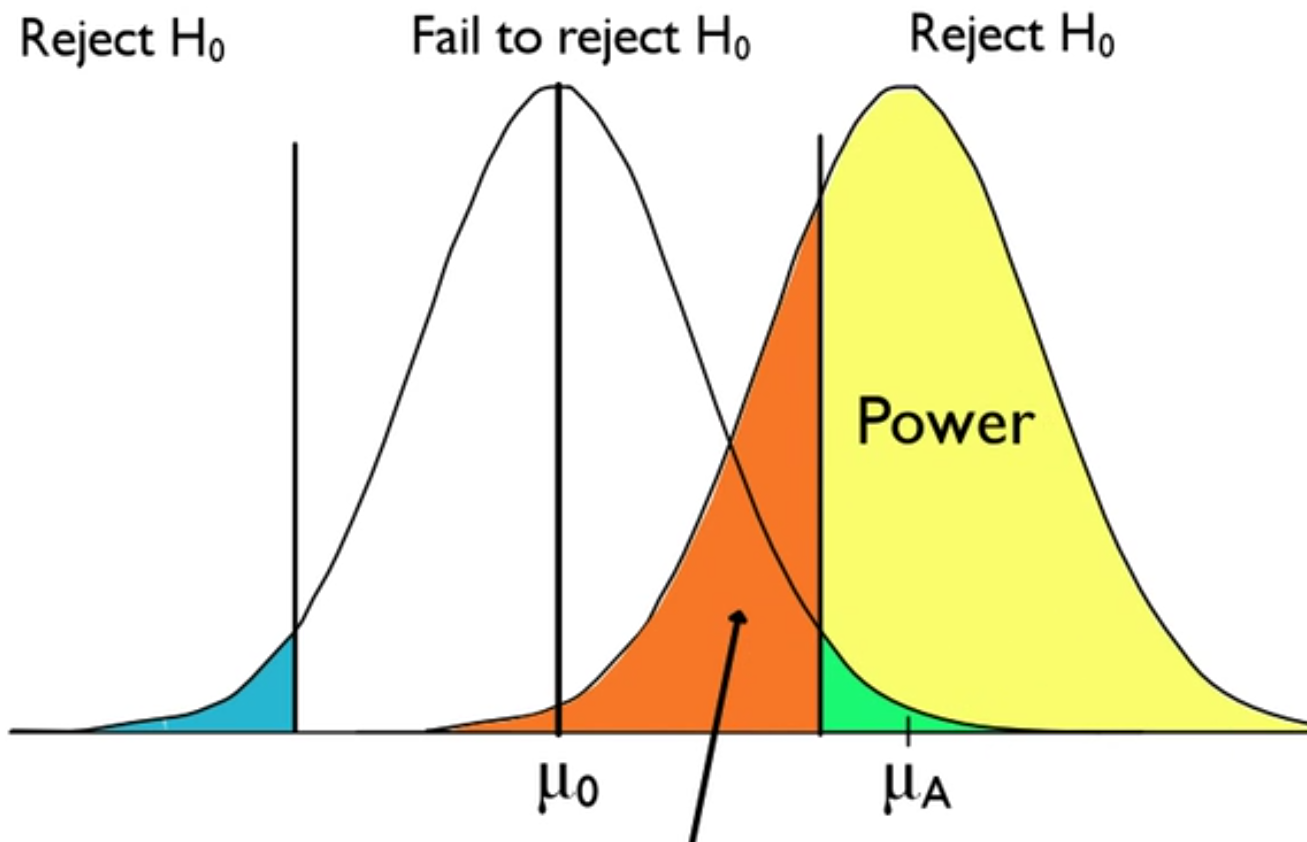
Now, the area in yellow on the other side, where you are correctly rejecting the null hypothesis when a difference is present, is called power of a hypothesis test. Power is the probability of rejecting the null hypothesis correctly, rejecting when the null hypothesis is false, which is a correct decision.
Source: Adapted from Sophia tutorial by Jonathan Osters.