Simplifying Rational Expressions

1. Simplifying Numeric Fractions

When first learning how to simplify rational expressions (or algebraic fractions), it can be very helpful to review how we simplify numeric fractions (containing no variables). This is because the thought process is the same. The only difference is that we have variables and algebraic factors to consider when simplifying rational expressions.

EXAMPLE

Simplify the fraction .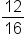

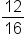
To simplify this fraction, we break both the numerator and denominator down into their prime factors. From there, we see what factors appear in both the numerator and denominator, and remove them from the fraction completely. What we are left with is the simplified fraction:

	Break numerator and denominator into prime factors
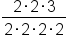
	Two factors of 2 cancel
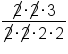
	Simplify
	Evaluate
	Our simplified fraction

2. Simplifying Rational Expressions with Factored Polynomials

The same principle applies to simplifying rational expressions. We look for common factors in both the numerator and denominator and cancel them. The only tricky there here is identifying those common factors, and in some cases, not confusing them for terms.

EXAMPLE

Simplify the expression .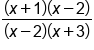

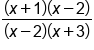
	The factors cancel
	Simplify
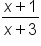
	Our solution

hint

Be careful here. Many people make the mistake of thinking that x is a common factor. Here, x is a term that is part of two entirely different factors. We cannot cancel part of a factor, we can only cancel out entire, complete factors. In other words, we cannot simplify the above fraction to 1/3.

3. Simplifying Rational Expressions by Factoring

Simplifying rational expressions would be so easy if all rational expressions were written in factored form. Unfortunately, this isn't the case. However, we may be able to write the numerator and denominator as factors, or at least factor out a few common factors, in order to cancel and simplify the expression.

EXAMPLE

Simplify the expression .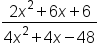

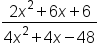
One strategy is to see if there is a common factor between all terms of the numerator, and a common factor between all terms in the denominator. Here, we see that a 2 can be factored out of each term in the numerator. We can also factor out a 4 in all of the terms in the denominator. Let's see how this helps us simplify:

	Factor out 2 in the numerator and 4 in the denominator
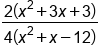
	Cancel 2 out of both numerator and denominator
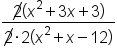
	Simplify
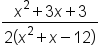
	Distribute denominator
	Our simplified fraction

hint

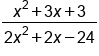
Even if we were to factor the numerator and denominator, there would be no more common factors, so we have found the simplified fraction.

Let's work through a final example, in which factoring the expressions in the numerator and denominator will lead to common factors:

EXAMPLE

Simplify .

	Factor out 6 in the numerator and 4 in the denominator
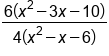
	6/4 simplifies to 3/2
	Factor the numerator and denominator
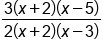
	The factors cancel
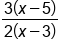
	Distribute both numerator and denominator
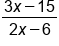
	Our simplified function

hint

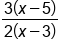You may choose to leave the fraction expression in factored form or in standard form 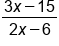. Both are considered fully simplified because all common factors have been canceled.