Simplifying Square Roots

1. Square Roots and Perfect Squares

The square root of a number is an operation or calculation that is performed on a number, resulting in a number whose product with itself is the original number.

EXAMPLE

The square root of 9 is 3, because 3 times 3 is 9.

You can find square roots in many areas of art, design, and engineering. The distance formula and Pythagorean theorem are significant geometric principles involving square roots. You also use square roots when solving quadratic equations, which can be used to model a ball or projectile under the influence of gravity.

You can refer to 9, as well as other numbers, as a perfect square because when you take the square root of the number, the answer is an integer. Therefore, perfect squares are also called squares of integers.

EXAMPLE

As you can see in the examples below, 7 squared is 49, and the square root of 49 is 7. Therefore, 49 is a perfect square. Similarly, 2 squared is 4, and the square root of 4 equals 2. So, 4 is a perfect square. Lastly, 5 squared equals 25, and the square root of 25 equals 5; 25 is also a perfect square.

Squares	Square Roots

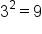
An example of a number that is not a perfect square is 20, because no integer squared equals 20, and because the square root of 20 is approximately 4.472, which is not an integer or whole number.

terms to know

Sqrt(x)

A number whose product with itself is x

Perfect Square

A number that is the square of a whole number

2. Product Property of Roots

To simplify square roots, you can find factors of the number inside the square root and break the expression into several square roots using the product property of roots.

In general, the product property of roots says that the square root of a times b is equivalent to the square root of a times the square root of b.

formula to know

Product Property of Roots

EXAMPLE

10 squared equals 100; therefore, you can see that the square root of 100 equals 10.



However, you can also determine this by using the product property of roots. The square root of 100 is equal to the square root of 4 times 25, so using the product property of roots, you know this is equal to square root of 4 times the square root of 25. This, in turn, is equal to 2 times 5, which equals 10.

The product property of roots also works for more than just two numbers, and is useful in simplifying square roots of numbers that are not perfect squares.

hint

Be careful not to assume that this also works for addition, because in general, the square root of a plus b is not equal to the square root of a plus the square root of b.

EXAMPLE

The square root of 4 plus 9 is equal to the square root of 13, which is approximately 3.606.



However, the square root of 4 plus the square root of 9 is equal to 2 plus 3, which is equal to 5. Therefore, you can see that there is no addition property of roots.

So, how can you simplify square roots that are not necessarily perfect squares? The product property is useful when simplifying the root of a number that is not a perfect square. It is important to note, however, that recognizing the perfect squares will help you simplify.

EXAMPLE

Suppose you want to simplify the square root of 50. 50 is not a perfect square, so you know that when you determine the square root of 50, your answer will not be an integer. However, you want to write 50 as a product of one or more perfect squares in order to simplify.

You know that 25 is a perfect square, so you can rewrite the square root of 50 as the square root of 25 times 2. Using the product property of roots, this expression is the same as the square root of 25 times the square root of 2. The square root of 25 is 5, so you now have 5 times the square root of 2.

did you know

It is standard to put the square root at the end of the expression.

IN CONTEXT

Suppose the baseball diamond in a stadium has an area of 8,100 square feet.



Since all the sides of the diamond have equal length, the area of the diamond can be represented with the formula A is equal to s squared, where s is the side length.



Since you know that the area is 8,100, you can plug this number into the formula, so that 8,100 equals s squared.



Next, to find the length of each side of the diamond, or the distance between each base, you can take the square root of each side of the equation, giving you the equation of the square root of 8,100 is equal to s.



Now you can simplify using the product property of roots. The square root of 8,100 is equal to the square root of 81 times 100. This, in turn, is equal to the square root of 81 times the square root of 100, which equals 9 times 10, or 90 feet.



Therefore, the side length, or the distance between bases in the baseball diamond, is approximately 90 feet.

3. Order of Operations with Square Roots

You can also simplify square roots using the order of operations, which is illustrated by the acronym PEMDAS to help you remember the correct order of operations. PEMDAS stands for:

Parentheses (and other grouping symbols)
Exponents
Multiplication
Division
Addition
Subtraction

Square roots and other radicals fall under the parentheses, since a square root acts as a grouping symbol when there are other operations underneath the square root. This means that the operations underneath the radical must be performed before taking the root.

EXAMPLE

Suppose you want to simplify the expression: .

	Our Expression
	Because the radical acts as a grouping symbol, we need to evaluate everything under it before we take the root. So we will start with the exponent. 4 squared equals 16.
	Next, we will multiply 12 and 3. This gives us 36.
	Now, we can add 36 and 16, which gives us 52.
	Now, we can simplify the square root. The square root of 52 can be written as the square root of 4 times 13, which is the same as the square root of 4 times the square root of 13.
	We can simplify the square root of 4 to be 2 times the square root of 13. Make sure that the square root of 13 is placed at the end of the expression.
	Our Solution

IN CONTEXT

Suppose you are on a vacation, traveling to a landmark that is 2 miles east and 4 miles south of your hotel. What is the straight line distance between your hotel and the landmark? You can use the Pythagorean theorem to determine this straight line distance.

The straight line distance, d, will be equal to the square root of 2 squared plus 4 squared.


You can start to simplify by evaluating your exponents and squaring 2 and 4. This gives you the square root of 4 plus 16. The square root of 4 plus 16 is the square root of 20, which can be written as the square root of 4 times 5. This is equivalent to the square root of 4 times the square root of 5, which is equal to 2 times the square root of 5.



Again, you would place the square root of 5 at the end of the expression. Therefore, the straight line distance between your hotel and the landmark is 2 times the square root of 5 miles.