Table of Contents |
Suppose a family has five children. What's the probability that at least two of those five are girls?
You could figure this out in a tree diagram, but that would be an unwieldy tree diagram. You can use a simulation to figure out complicated problems like this one. This is also called the Monte Carlo method, named after Monte Carlo Casino because it uses physical objects like dice.
Let's approximate the probability using a simulation. Get five dice out and let the boys and girls be equally likely. Let's have faces 1 through 3 represent girls, and 4 through 6 represent boys.
Roll #1:

On the first roll, you get two girls (the 1 and the 2).
Roll #2:

One the second roll, this situation has four girls in it--the 2, 3, 3, and 1. Redo this many times, and the relative frequency of getting two or more girls will approximate the probability.
Suppose you do this 20 times, then analyze the results in the chart below.
| Trial | Die 1 | Die 2 | Die 3 | Die 4 | Die 5 | Girls |
|---|---|---|---|---|---|---|
| 1 | 6 | 4 | 1 | 2 | 6 | 2 |
| 2 | 2 | 3 | 3 | 6 | 1 | 4 |
| 3 | 6 | 3 | 3 | 2 | 2 | 4 |
| 4 | 1 | 2 | 4 | 4 | 1 | 3 |
| 5 | 6 | 5 | 6 | 3 | 2 | 2 |
| 6 | 5 | 6 | 4 | 6 | 5 | 0 |
| 7 | 2 | 1 | 3 | 6 | 1 | 4 |
| 8 | 6 | 3 | 2 | 3 | 3 | 4 |
| 9 | 5 | 2 | 1 | 1 | 2 | 4 |
| 10 | 2 | 5 | 3 | 4 | 1 | 3 |
| 11 | 6 | 1 | 5 | 2 | 4 | 2 |
| 12 | 1 | 2 | 1 | 6 | 5 | 3 |
| 13 | 2 | 6 | 5 | 5 | 2 | 2 |
| 14 | 3 | 6 | 1 | 5 | 1 | 3 |
| 15 | 6 | 3 | 5 | 2 | 2 | 3 |
| 16 | 6 | 2 | 1 | 4 | 1 | 3 |
| 17 | 4 | 5 | 3 | 5 | 1 | 2 |
| 18 | 2 | 3 | 3 | 6 | 1 | 4 |
| 19 | 4 | 4 | 1 | 6 | 2 | 2 |
| 20 | 6 | 6 | 2 | 1 | 6 | 2 |
As you can see in the chart, in the first trial, you got a 6, 4, 1, 2, and 6, which represented two girls. In one situation, you didn't get any girls in your group of five.
This is the histogram of the number of girls per family.
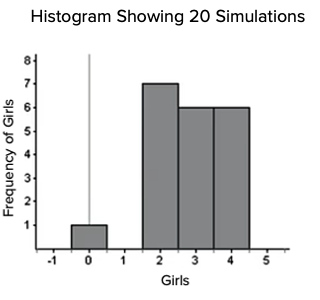
It is fairly unusual that you didn't get exactly one girl in any of the simulations. The most common was two girls; three and four were also very common. You got at least two girls in 19 of the 20 simulations. Your guess for the probability of having at least two girls in a family is 19 out of 20, or 95%. Your best guess is that you have a 95% probability of getting at least two girls in a family.
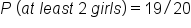
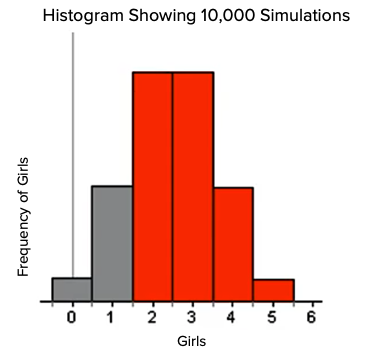
The right answer is, in fact, 0.8125, about 81% of the time. If you simulated more than 20 times with the dice, you would have gotten a more accurate response. So our sample of 20 was not truly representative. Apparently, having four girls is fairly uncommon. Two and three are very common.
Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.