Table of Contents |
A rational equation is an equation that contains at least one rational expression. Recall that a rational expression can also be referred to as an algebraic fraction. In other words, one of the terms has a variable in the denominator.
There is a very important implication when a variable is in the denominator of an expression or equation. Dividing any quantity by zero leads to an undefined value, so whenever the denominator is equal to zero, the equation is undefined. Sometimes, when solving rational equations, we can make all the right moves algebraically, but the solution we get for our variable makes our denominator equal to zero. These solutions are known as extraneous solutions.
A useful strategy in solving rational equations is to rewrite the equation so that every term has a common denominator. The reason for this is that once all terms are written to have a common denominator, we can create an equation with just the numerators.
EXAMPLE
Find the solution to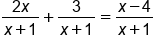 .
.
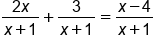
|
Use numerators only |
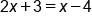
|
Subtract 3 from both side |
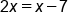
|
Subtract x from both sides |
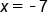
|
Our solution |
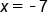 , we never have a denominator of zero in any of the terms. Since the denominator is
, we never have a denominator of zero in any of the terms. Since the denominator is  , and
, and 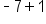 is equal to -6, which is non-zero, we can say that
is equal to -6, which is non-zero, we can say that 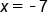 is the solution to this rational equation.
is the solution to this rational equation.
Now that we have a useful strategy for solving rational functions, let's talk about the processes for creating terms with common denominators. The easiest method to find a common denominator between rational expressions is to multiply the terms in the denominator together.
EXAMPLE
Find a common denominator between these algebraic fractions:
 ,
,  , and
, and  , together.
, together.
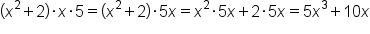
 .
.
This method works for all cases, but it can get a bit messy sometimes with algebraic fractions. One strategy is to find the lowest common denominator by factoring each expression and multiply all of the distinct factors.
EXAMPLE
Find the least common denominator between these algebraic fractions: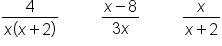
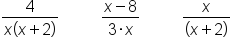
 . This is used once in the first fraction and once in the third fraction, so the greatest number of times it is used is once. So
. This is used once in the first fraction and once in the third fraction, so the greatest number of times it is used is once. So  will also be included in the lowest common denominator:
will also be included in the lowest common denominator:

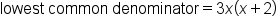
Once we have our common denominator, we can solve for equation by following these steps:
Let's solve the following rational equation using our common denominator strategy:
EXAMPLE
Find the solution to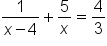 .
.
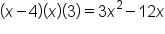

|
The denominator needs factors 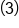 and and  ; multiply both numerator and denominator ; multiply both numerator and denominator
|
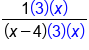
|
Evaluate multiplication |

|
Equivalent fraction to 
|
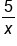
|
The denominator needs factors 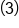 and and  ; multiply both numerator and denominator ; multiply both numerator and denominator
|
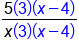
|
Evaluate multiplication |

|
Equivalent fraction to 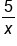
|
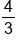
|
The denominator needs factors  and and  ; multiply both numerator and denominator ; multiply both numerator and denominator
|
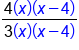
|
Evaluate multiplication |
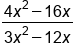
|
Equivalent fraction to 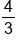
|
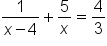
|
Multiply each fraction by the other denominators |
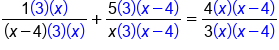
|
Evaluate multiplication |

|
Create equation with just numerators; ignore denominators |
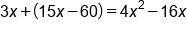
|
Equation with just numerators |
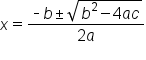 , once we set one side of the equation equal to zero:
, once we set one side of the equation equal to zero:
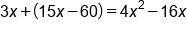
|
Combine 3x and 15x on the left side |

|
Subtract 18x and add 60 to both sides |
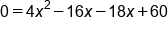
|
Combine -16x and -18x on the right side |
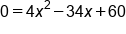
|
Identify coefficients  b, and c b, and c
|
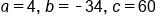
|
Plug these values into quadratic formula |

|
Evaluate |
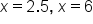
|
Our solutions |
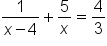
|
Plug in 2.5 for x |
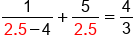
|
Evaluate |

|
Plugging 2.5 in for x does NOT result in any denominator of zero, so this is NOT an extraneous solution |
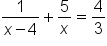
|
Plug in 6 for x |

|
Evaluate |

|
Plugging 6 in for x does NOT result in any denominator of zero, so this is NOT an extraneous solution |
 or
or 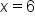 , there are no extraneous solutions to the rational equation.
, there are no extraneous solutions to the rational equation.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License