Solving a Quadratic Equation using the Quadratic Formula

1. Quadratic Equations: A Review

In review, a quadratic equation is an equation that can be written in the following form, where a, b, and c are real numbers:

Factoring, or variable isolation, may be used to solve some quadratic equations, but not all. The quadratic formula, however, can be used to find solutions to all quadratic equations, even when factoring or variable isolation is difficult or impossible. Therefore, sometimes it is necessary to use the quadratic formula to find solutions to a quadratic equation.

2. The Quadratic Formula: A Review

You may recall that the quadratic formula states that the solution(s) to a quadratic equation, x, are equal to:

formula to know

Quadratic Formula

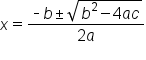
The values for a, b, and c in the quadratic formula come from the values of a, b, and c in the quadratic equation. The plus-minus symbol here indicates that a quadratic equation may have two solutions.

did you know

When working with the quadratic formula, you often have to simplify square roots using the product property, as shown below, or by recognizing perfect squares.

formula to know

Product Property of Roots

3. Solving Quadratic Equations with the Quadratic Formula

EXAMPLE

Suppose you want to solve the quadratic equation:



You can solve this equation using the quadratic formula. From the equation, you can see that there is no written number in front of , meaning that there is an implied coefficient of 1. Therefore, a equals 1. You can also see that b equals 7 and c equals -4.



Substituting these values into the formula provides:



You can simplify the numerator and the denominator separately. Simplifying the denominator is simple:



Next, you can simplify the numerator, which is more complicated, because it involves the plus-minus symbol, square roots, and other operations. You start underneath the square root. moving left to right. is 49, and 4 times -1 is -16. You now have 49 minus -16, which is the same as 49 plus 16, which equals 65. The square root of 65 cannot be further simplified, so you’d leave it as written.



You now have the following solution, which can be separated into its two parts by separating the plus and the minus symbols.



You can further simplify both of these fractions into two separate fractions each:

try it

Consider the following quadratic equation:

Use what you’ve learned so far to solve the following quadratic equation, using the quadratic formula.

From the equation, you can see that:

• a = 2
• b = -8
• c = -3

Notice that b is already a negative number, so when you substitute it into the formula, you have -(-8), which is +8.



Start by simplifying in the denominator:



Next, simplify in the numerator, starting with the operations underneath your square root.



Now you can simplify the square root of 88 as the square root of 4 times the square root of 22, using the product property of radicals. The square root of 4 is 2, so your solution is:



You can separate this into two solutions:



You can also separate each of these solutions into separate fractions:



In this form, you can see that you can simplify these fractions further, so your fully simplified solutions are: