Table of Contents |
A solution to a system of linear equations is a specific coordinate (x, y) that satisfies all equations in the system. Graphically, the solution, then, is the intersection point of all lines in the system. The intersection between all lines in the system represents a single (x, y) coordinate that satisfies all equations in the system.
A few cautions about solving with a graph: accuracy is key. If the scale or graph is not easily read, you may end up with only approximate answers, rather than exact solutions to the system.
For some systems of equations, only a graph is provided, rather than the equations.
The graph below shows two lines that make up a system of equations.
EXAMPLE
What is the solution to the following system of equations?
 and
and 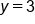 will satisfy both equations in our system.
will satisfy both equations in our system.
However, take a look at this next graph which shows three lines that make up a system of equations:
EXAMPLE
What is the solution to the following system of equations?
How can you use a graph to solve a given system of equations? You'll first take the equations in the system, graph each equation, and look for the intersection point.
EXAMPLE
Solve the following system of equations by graphing:

|
For the first equation, find the x-intercept by plugging in 0 for y |

|
Subtract 0 from 2x |

|
Divide both sides by 2 |

|
The x-coordinate to the x-intercept |
 is (-2, 0).
is (-2, 0).

|
For the first equation, find the y-intercept by plugging in 0 for x |

|
Multiply 2 and 0 |

|
Divide both sides by -1 |

|
The y-coordinate to the y-intercept |
 is (0, 4).
is (0, 4).


|
For the second equation, find the x-intercept by plugging in 0 for y |

|
Add 0 and x |

|
The x-coordinate to the x-intercept |
 is (7,0).
is (7,0).

|
For the second equation, find the y-intercept by plugging in 0 for x |

|
Add 0 and y |

|
The y-coordinate to the y-intercept |
 is (0, 7).
is (0, 7).

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License