Table of Contents |
A solution to a system of linear equations is a specific coordinate pair (x, y) that satisfies all equations in the system. It is important that the solution satisfies every equation in the system, not just one; otherwise, it doesn't represent a solution to the entire system.
There are several ways to find solutions to a system of linear equations, such as by graphing or using the addition method. This lesson focuses on a different method known as the substitution method.
The main goal of the substitution method is to rewrite one of the equations so that one variable is isolated on one side of the equation, with everything else on the other side. As a result, that equivalent expression for the variable can be substituted into other equations in the system, in order to make solving for a particular variable possible. Once we find a value for one of the variables in a system, it becomes much easier to solve for other variables in the system.
Before we get into an example of using the substitution method to solve a system of equations, let's go over some general rules and tips.
It does not matter which equation or which variable you choose to isolate. As long as you don't make any algebraic errors, your answer will be the same no matter which route you choose. However, some choices are better than others, as they lower the chances of making algebraic errors. Keep these things in mind:
EXAMPLE
Use the Substitution Method to find the solution to the following system of equations: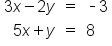
 or
or  . Remember one of our helpful hints: choosing a variable term with no coefficient will reduce the number of steps, and make our calculations less complicated. For this reason, we are going to take the equation
. Remember one of our helpful hints: choosing a variable term with no coefficient will reduce the number of steps, and make our calculations less complicated. For this reason, we are going to take the equation 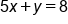 , and rewrite it as
, and rewrite it as  . This will be the easiest because y is already isolated in this equation:
. This will be the easiest because y is already isolated in this equation:
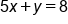
|
Using the second equation, subtract 5x from both sides |
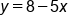
|
An equivalent equation to the original |
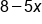 :
:

|
Using the first equation, substitute 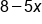 for y for y
|
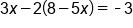
|
Distribute -2 into 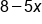
|
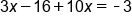
|
Combine 3x and 10x |
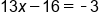
|
Add 16 to both sides |
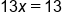
|
Divide both sides by 13 |

|
Our solution for x |
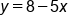
|
Using the equivalent equation, plug 1 in for x |
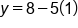
|
Multiply 5 and 1 |
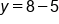
|
Subtract 5 from 8 |
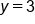
|
Our solution for y |
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License