Table of Contents |
When solving an equation, our main goal is to isolate the variable we wish to solve for onto one side of the equation, and then evaluate the expression on the other side of the equation. To do this, we use inverse operations to undo the operations on our variable. With single step equations, only one operation is applied to our variable, so only one inverse operation must be applied. Let's review these inverse operations.
| Operation | Inverse Operation |
|---|---|
| Addition | Subtraction |
| Subtraction | Addition |
| Multiplication | Division |
| Division | Multiplication |
| Powers | Roots |
| Roots | Powers |
What do we do when we have several operations being performed on the variable we wish to solve for? We know that we must perform inverse operations to both sides of the equation (due to the Rule of Equality for equations), but in what order? Think about the order of operations. These operations are applied to the variable following the order of operations. To undo this, we apply inverse operations in the reverse order of operations
Generally, there are two options when you have an equation involving distribution.
EXAMPLE
Solve the equation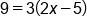 using both options.
using both options.
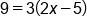
|
Divide both sides of the equation by 3 |
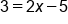
|
Undo -5 by adding 5 to both sides of the equation |
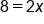
|
Undo multiplication of 2 by dividing both sides by 2 |
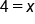
|
Our Solution |
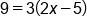
|
Distribute 3 on the right side |

|
Undo subtracting 15 by adding 15 to both sides |
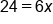
|
Undo multiplication of 6 by dividing both sides by 6 |
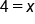
|
Our Solution |
When a variable appears in the denominator of a fraction, it can be difficult to isolate that variable until it is moved into a numerator. When the denominator contains the variable, the first step we take is to multiply the entire equation by the expression in the denominator. This eliminates the variable from the denominator on one side of the equation, and makes it part of the numerator on the other side of the equation.
EXAMPLE
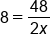
|
Multiply both sides of the equation by 2x |

|
2x’s on the right side will cancel, leaving 48. |
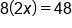
|
Multiply 8 and 2x |
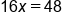
|
Divide both sides by 16 |

|
Our Solution |
So far we have seen how to apply inverse operations to undo addition, subtraction, multiplication and division. Lastly, let's see how to apply power and roots to solve a multi-step equation.
EXAMPLE
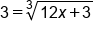
|
Undo the cube root by cubing both sides |
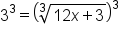
|
Cubing a cubed root will leave only  on the right side; Evaluate on the right side; Evaluate 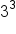
|
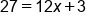
|
Undo the addition of 3 by subtracting 3 from both sides |

|
Undo the multiplication of 12 by dividing both sides by 12 |
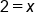
|
Our Solution |
As we can see with the example above, we had an expression underneath a cube root. To undo this, we cubed both sides of the equation. We were left with the expression alone, without a radical, and 3 cubed on the other side. From there, we were able to solve for x by applying our familiar inverse operations.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License