Table of Contents |
There are several ways we can talk about solutions to quadratic equations. Solutions are also called roots or zeros because they represent x-values to the equation that makes y equal to zero. Below is a graphical representation of solutions to a quadratic equation:
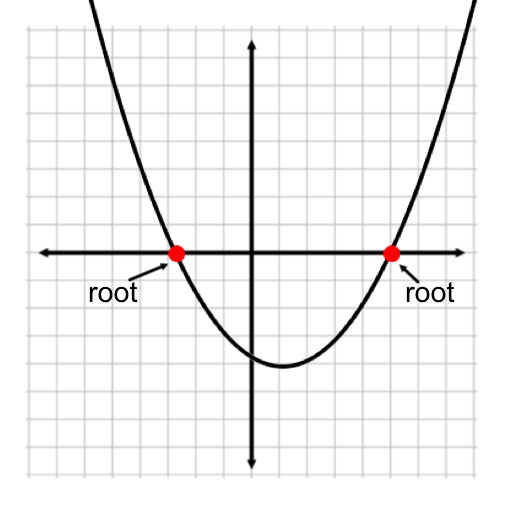
| Two Solutions | One Solution | No Solutions |
|---|---|---|

|

|

|
| Solutions: (-2, 0) and (5, 0) | Solutions: (-3, 0) | No Real Solutions |
If any factor of an algebraic expression equals zero, the entire expression has a value of zero. This is because any quantity multiplied by zero is zero. This fact comes in handy when solving quadratic equations written in standard form. We can simply set each factor equal to zero, and solve simpler equations to find solutions to the quadratic.
EXAMPLE
Find the solutions for the quadratic equation .
.

|
Factor the left side of the equation by finding two numbers that multiply to -21 and add to -4 |
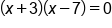
|
Set each factor equal to zero |
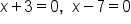
|
Solve for x in each factor |

|
Our solutions |
 the quadratic will equal zero:
the quadratic will equal zero:
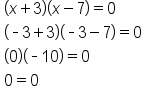
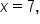 the quadratic will equal zero:
the quadratic will equal zero:

When a quadratic is set equal to zero, but has no constant term, making use of the Zero Factor Property is still helpful, but there is some work that needs to be done first. Without the constant term, we know that all of the terms in the quadratic share a factor of x. This means we can factor it out, and then apply the Zero Factor Property.
EXAMPLE
Find the solutions for the quadratic equation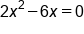 .
.
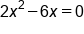
|
Factor out x |
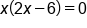
|
Set each factor equal to 0 |
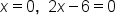
|
Solve for x in each factor |
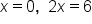
|
Further simplify the second factor |
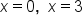
|
Our solutions |
 :
:
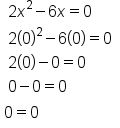
 :
:
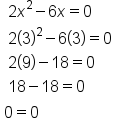
If a quadratic equation is missing an x-term, using the Zero Factor Property is not as helpful. Instead, we can solve using standard algebraic techniques for solving any equation. The important thing to remember here is that when we apply the square root to a quantity squared, we must include both positive and negative values of the root because a negative value squared is also positive.
EXAMPLE
Find solutions to the quadratic equation .
.

|
Move the constant to the right side by adding 7 to both sides |
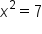
|
Apply square root to both sides |
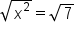
|
Evaluate |
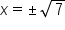
|
Don't forget to include both positive and negative solutions |
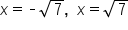
|
Our solutions |
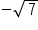 and
and 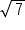 evaluate to 7 when squared.
evaluate to 7 when squared.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License