Table of Contents |
When graphing a linear inequality, we follow a similar process to graphing a linear equation. In fact, we can first think of the inequality as an equation, with an equals sign rather than an inequality symbol, and graph the line. When we do this, what we are really doing is graphing the boundary line to the inequality. To correctly graph the boundary line, we need to consider whether the inequality symbol is strict or non-strict:
| Type | Symbol | Boundary Line |
|---|---|---|
| Strict | < or > | Dashed |
| Non-Strict | ≤ or ≥ | Solid |
We also need to shade half of the coordinate plane when graphing an inequality, to show which coordinate pairs (x, y) represent solutions to the inequality. When boundary lines are written in the form 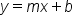 , the type of inequality symbol tells us to shade either above or below the line:
, the type of inequality symbol tells us to shade either above or below the line:
| Description | Symbol | Shade... |
|---|---|---|
| "less than" or "less than or equal to" | < or ≤ | Shade below (or to the left) |
| "greater than" or "greater than or equal to" | > or ≥ | Shade above (or to the right) |
When graphing a system of inequalities, we have more than one inequality graphed on the same coordinate plane. Solution regions to individual inequalities will overlap with other solution regions, but not necessarily all other solution regions. A solution to the entire system of inequalities is the overlap of all of the individual solution regions.
Let's solve a system of inequalities using a graphical approach, rather than using algebraic techniques to solve. To do so, we will plot each inequality individually, along with its solution region. Then, we will analyze the graph to determine if there exists an overlap between all solution regions to the inequalities that make up our system.
EXAMPLE
Solve the following system of inequalities by graphing: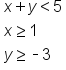
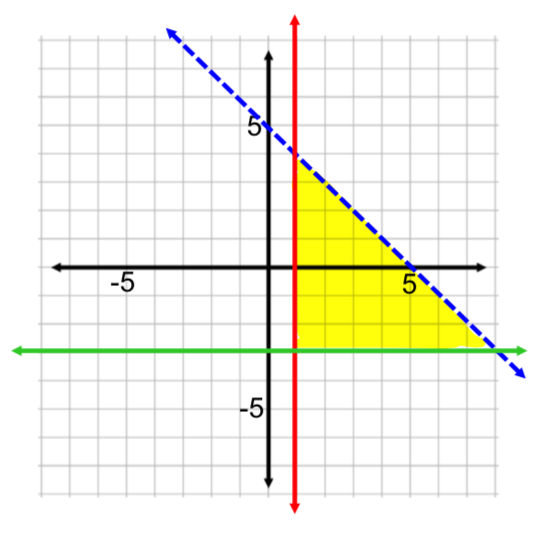
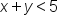 , we take note of the strict inequality symbol, which tells us to use a dashed line to graph the boundary line
, we take note of the strict inequality symbol, which tells us to use a dashed line to graph the boundary line 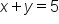 . This linear equation is in standard form, so we can graph this line by finding the x- and y-intercepts. Alternatively, you could change this into slope-intercept form and graph it that way. Using standard form, when
. This linear equation is in standard form, so we can graph this line by finding the x- and y-intercepts. Alternatively, you could change this into slope-intercept form and graph it that way. Using standard form, when  , then
, then  , so the x–intercept is the point (5, 0). Similarly, when
, so the x–intercept is the point (5, 0). Similarly, when  , then
, then 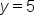 , so the y–intercept is (0, 5). Plot these two points and connect them with a dashed line.
, so the y–intercept is (0, 5). Plot these two points and connect them with a dashed line.
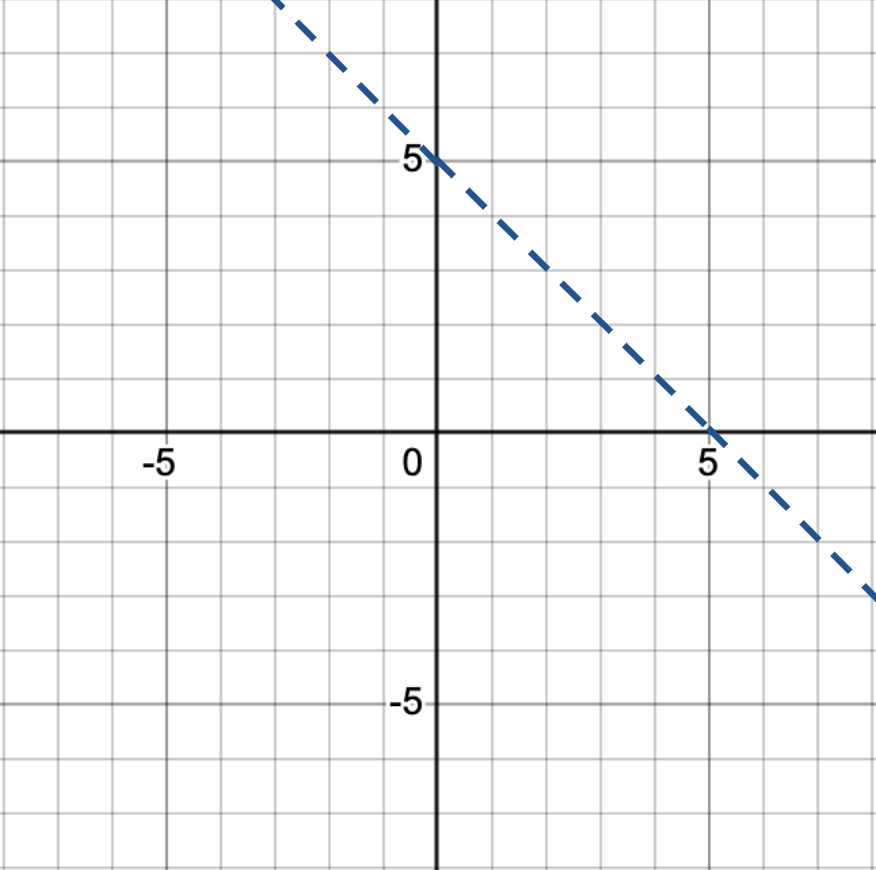
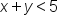 , we should use a test point.
, we should use a test point.
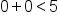 is a true statement (because 0 is less than 5), the point (0, 0) lies within the solution region, and we shade the half-plane that includes this point.
is a true statement (because 0 is less than 5), the point (0, 0) lies within the solution region, and we shade the half-plane that includes this point.

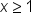 to our graph. This inequality is quite simple to graph because it is a vertical line. We'll just take note of our inequality symbol to determine what kind of line to draw, and which region to shade. Our inequality symbol is non-strict, so we use a solid line, and we'll shade to the right of the line because that represents greater x-values.
to our graph. This inequality is quite simple to graph because it is a vertical line. We'll just take note of our inequality symbol to determine what kind of line to draw, and which region to shade. Our inequality symbol is non-strict, so we use a solid line, and we'll shade to the right of the line because that represents greater x-values.
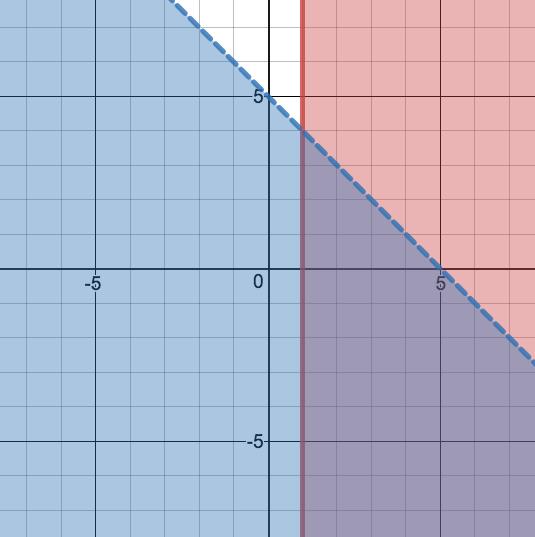
 , it is also quite simple to graph as it is a horizontal line. We once again look at the inequality symbol: it is non-strict, so we will use a solid line to draw the boundary line. Since the symbol is "greater than or equal to" we also know to shade above the boundary line.
, it is also quite simple to graph as it is a horizontal line. We once again look at the inequality symbol: it is non-strict, so we will use a solid line to draw the boundary line. Since the symbol is "greater than or equal to" we also know to shade above the boundary line.
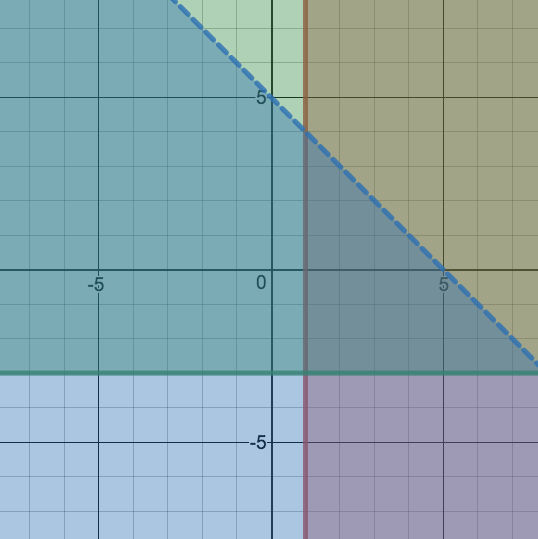
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License