Table of Contents |
Our special products of binomials come through by noticing how expressions are simplified in binomial multiplication. Binomial multiplication is often modeled through a process known as FOIL, which is an acronym that stands for First, Outside, Inside, Last. It describes an order to multiply terms that make up the two factors in binomial multiplication.
EXAMPLE
Multiply .
.

|
Multiply first terms: 
|

|
Multiply outside terms: 
|

|
Multiply inside terms: 
|

|
Multiply last terms: 
|

|
Combine like terms |

|
Our solution |
Take a look at what happens when we expand a binomial sum that is being squared:
EXAMPLE
Multiply .
.

|
Rewrite as multiplication of two factors, 
|

|
FOIL |
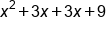
|
Combine like terms |

|
Our solution |
Note the relationship between the constant in our binomial sum (3), the coefficient of the x-term (6), and the constant term in the expanded trinomial (9). See if the relationship you spotted holds true in another example:
EXAMPLE
Multiply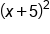 .
.
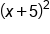
|
Rewrite as multiplication of two factors, 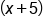
|
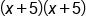
|
FOIL |
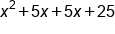
|
Combine like terms |

|
Our solution |
What is the relationship between 5, 10, and 25? If we take the constant from the binomial sum, 5, and double this number, we get the coefficient of x-term, 10. And if we square 5, we get 25, which is the constant term in the expanded trinomial. This holds true for all squares of binomial sums.

Test it out with a few more examples:
| Original Expression | Coefficient of x-term | Constant | Expanded Expression |
|---|---|---|---|
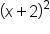
|
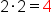
|
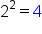
|

|
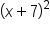
|

|
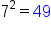
|

|

|
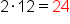
|

|

|
Next, let's take a look at similar expressions, except these examples involve subtraction instead of addition:
EXAMPLE
Multiply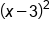 .
.
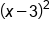
|
Rewrite as multiplication of two factors, 
|
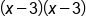
|
FOIL |

|
Combine like terms |
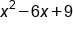
|
Our solution |
Note that the only distinction here is that the x-term is a negative 6x, because we subtracted 3 from x in the binomial. We still have +9 because -3 times -3 is a positive number. Let's take a look at another example:
EXAMPLE
Multiply .
.

|
Rewrite as multiplication of two factors, 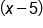
|
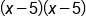
|
FOIL |
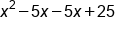
|
Combine like terms |
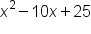
|
Our solution |
We can generalize this as the square of a binomial difference:
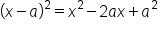
Test it out with a few more examples:
| Original Expression | Coefficient of x-term | Constant | Expanded Expression |
|---|---|---|---|

|
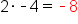
|

|
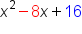
|

|
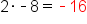
|

|

|
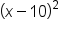
|

|
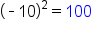
|

|
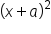 or
or 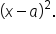
So far we have discussed special products involving a binomial squared, where a is either positive or negative. We can have a binomial sum  or a binomial difference
or a binomial difference 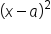 . Now, we are going to consider the case where we have a binomial sum multiplied by a binomial difference.
. Now, we are going to consider the case where we have a binomial sum multiplied by a binomial difference.
EXAMPLE
Multiply .
.

|
FOIL |
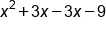
|
Combine like terms |
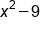
|
Our solution |
There are a couple of things to note in this example:
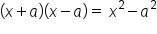
Test it out with a few more examples:
| Original Expression | Coefficient of x-term | Constant | Expanded Expression |
|---|---|---|---|
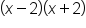
|

|
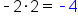
|

|
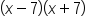
|
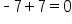
|
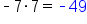
|
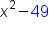
|
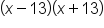
|
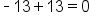
|
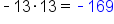
|

|
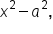 which can be expressed as
which can be expressed as 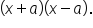
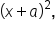 square of a binomial difference:
square of a binomial difference: 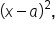 and the difference of squares:
and the difference of squares:  A perfect square trinomial is a polynomial with three terms that can be simplified as a binomial squared.
A perfect square trinomial is a polynomial with three terms that can be simplified as a binomial squared.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License