Table of Contents |
Z-scores are values that allow you to make one-to-one comparisons between a couple of different distributions. Often, you want to compare two things, but it's not really fair to compare them directly. Z-scores help with this.
A z-score is a value that explains how many standard deviations away from the mean an observation is. It can be positive (if the value is above the mean) or negative (if the value is below the mean).
IN CONTEXT
Suppose you are taking a math class. For the first exam of the year, the class mean was 88 points, and the standard deviation was 5. You scored a 92, so you did better than the class average. The second test was much harder. You scored an 80, which is a lot worse than you did the first time, but the class mean was 74. So, even though your score went down, the class average also went down. The standard deviation, this time, was 4 points. Did you do better on the first or the second test, relative to your classmates?
It's obvious that you scored higher on the first test, but relative to your classmates, did you do better on the first test or the second test? Just based on the scores, it's not fair to say that you did better on the first test. You want to see how you did relative to your classmates. Z-scores are going to allow you to make this comparison.
Z-scores are sometimes called standardized scores because they measure how many standard deviations away from the mean your observation is. In the previous example, for the first test of the year, the standard deviation was 5 for the first exam. You scored 4 points higher than average, 92 compared to the average score of 88. This means that your z-score is less than 1 because you are less than one standard deviation above the mean.
In the above example, the actual z-score for the first test is positive 4/5: positive 4 means above the mean, and divided by 5, the standard deviation.
But how do you get this calculation? You use this formula:

| Comparing Z-Scores of Two Tests | ||
|---|---|---|
| Test 1 |
The class mean is 88 with a standard deviation of 5. You score a 92. |

|
| Test 2 |
The class mean is 74 with a standard deviation of 4. You score an 80. |

|
The other thing that's worth noting is that a z-score can be negative. If you're subtracting a bigger number from a smaller number (i.e., if the raw score is a smaller number than the mean), then you'll end up with a negative value.
How are z-scores used in standard distributions? Let's explore an example.
EXAMPLE
Men's heights follow a normal distribution, with a mean of 68 and a standard deviation of 3.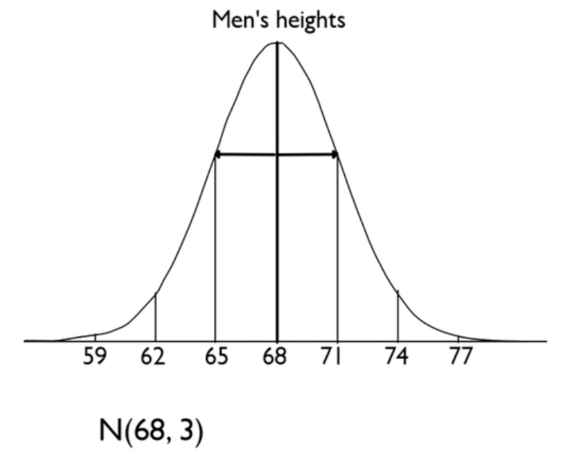


Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.