Sum of a Geometric Sequence in the Real World

1. Sum of a Finite Geometric Sequence in the Real World

Periodically contributing to a savings or investment account is a great way to increase your wealth, prepare for unexpected emergencies, or plan for the future. We may be able to model the growth of such an account using a geometric sequence.

EXAMPLE

Suppose we start out by investing $1200 into an account. This account gains 3.5% interest each year, which is applied at the end of the year. At the beginning of each year, we add another $1200 to the account. As this pattern continues, we have $1200 being added to the account each year, and 3.5% interest applied to the balance of the account after each year.

The first term of the sequence, , is going to be the initial deposit of $ 1200.

Geometric Sequence:

The second term of the sequence is going to be , or . This represents the first year's deposit with 3.5% interest. With two terms in the sequence now, the first term actually has a different meaning. It now represents the $1200 that is added after Year 1 (and it hasn't gained any interest yet, because it has just been deposited).

Geometric Sequence:

If we add the two terms together, we have a value of $2442, which represents two deposits of $1200, one of which has been in the account for a year, and thus has gained 3.5% interest.

Let's think about the third term in the sequence. We take the second term, $1242, and multiply it once again by 1.035 to show its growth. The third term has a value of $1285.47. This represents the initial deposit (now made 2 years ago) that has gained 3.5% interest for two years.

Geometric Sequence:

The second term now represents the $1200 deposit that was made one year after the initial deposit, and has gained 3.5% interest for only one year. The first term always represents the most recent deposit of $1200, having gained no interest.

As we can see, when we add the terms together, we are finding the value of the account after n deposits, assuming no other deposits or withdrawals are made (and that the interest rate is fixed).

Suppose we want to find the value of the account after the 7th deposit, also keeping these assumptions? We can use the formula for the sum of a finite geometric sequence to answer this question.

formula to know

Sum of a Finite Geometric Sequence

In this formula,

• is the sum of n terms (in this context, the balance of the account after n years).
• is the value of the first term in the sequence (in this context, the starting value of the account).
• r is the common ratio (in this context, it is the growth factor, 1 plus the annual percent rate, expressed as a decimal).
• n is the number of terms (in this context, it is the number of years).

EXAMPLE

Let's go back to the same scenario above and find the value of the account after the 7th deposit. In this example, we know the following values:

• (starting value of the account, $1200)
• (growth factor of the account, 1 plus annual percent rate of 3.5%)
• (number of years)

	Plug in
	Evaluate the exponent
	Simplify the numerator and denominator
	Evaluate the fraction
	Multiply
	Our solution

This means that after the 7th deposit, the account will have a balance of $9,335.29

2. Sum of an Infinite Geometric Sequence in the Real World

Let's now look at an infinite geometric sequence, where the terms in the sequence get closer and closer to zero.

EXAMPLE

Imagine a marble rolling across the floor. Measuring the distance the marvel travels in constant intervals, we notice that the marble travels half of the distance traveled in the previous interval. As the marble continues to roll, it will travel shorter and shorter distances within these time intervals, and will eventually travel a distance of virtually zero. This means that the total distance traveled (or the sum of all of the recorded distances) will converge to a specific distance.

The following sequence describes the distances traveled during each time interval, measured in centimeters:

How far does the marble travel in total? To answer this question, we will need to find the sum of this infinite geometric sequence.

As you recall, we have already defined this formula in a previous lesson.

formula to know

Sum of a Infinite Geometric Sequence

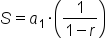
EXAMPLE

Let's go back to same scenario with the marbles and find the sum of the sequence. We can define the following variables:

• (the initial term is 80)
• (common ratio between each term is one half, or 0.5)

Plug these values into the formula

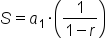
	Plug in
	Evaluate denominator
	Evaluate fraction
	Multiply
	Our solution

This means that the total distance traveled by the marble will eventually converge to 160 centimeters.

summary

Geometric sequences can be used to model real world situations such as the value of a bank account and the rate of change of velocity of an object in motion. In the formulas for the sum of a finite geometric sequence, and the sum of an infinite geometric sequence, is the first term in the sum, r is the common ratio between consecutive terms, and n is the number of terms.