Sum of an Infinite Geometric Sequence

1. Divergent Sequences and Series

A divergent sequence is a sequence whose terms do not have a finite limit. This means that as the sequence continues, the value of the terms will tend toward positive or negative infinity.

EXAMPLE

Consider the sequence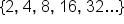 . As we continue to list terms in this sequence, we note that there will never be a definite limit to what the term might be, as the value of the terms become infinitely large.

This is also true when the common ratio is less than -1. The terms will alternate between positive and negative, but the absolute magnitude of the terms will head toward the infinities.

EXAMPLE

Consider the sequence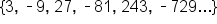 . As we continue to list terms in this sequence, there is not a definite limit to what the term will be. It will continue to alternate between negative infinity and positive infinity.

When it comes to summing an infinite divergent sequence, we find that there is not a concrete value to the sum, due to the fact that the terms themselves have no limit to their value. We refer to the sum of a sequence as a series. So if we have a divergent sequence, we also have a divergent series, since the sum also tends towards either positive or negative infinity.

Therefore, when we talk about the sum of infinite geometric sequences, we are working primarily with convergent sequences, or sequences with a common ratio between -1 and 1.

big idea

Because the terms in divergent sequences tend toward positive or negative infinity, the series is also divergent. For this reason, the formula for the sum of an infinite geometric sequence, which we will explore below, applies only to convergent sequences, where the common ratio is between -1 and 1.

2. Convergent Sequences and Series

Unlike divergent sequences, the terms in a convergent sequence tend toward a specific value. Since the common ratio in convergent sequences is between -1 and 1, as we continue to list terms in the sequence, the value actually tends toward zero.

EXAMPLE

Notice how the terms in the convergent sequence tend toward zero as we go further into the sequence.

When it comes to summing the terms in a convergent sequence, since we will eventually be adding virtually zero, this also means that the series converges to a specific value as well.

3. The Formula for the Sum of an Infinite Geometric Sequence

You may be familiar with the formula for the sum of a finite geometric sequence when the number of terms in the sequence is clearly defined, rather than never-ending. The formula for that is:

formula to know

Sum of a Finite Geometric Sequence

In this formula:

• is the sum of n terms
• is the value of the first term
• is the common ratio
• is the number of terms

EXAMPLE

Consider a sequence that has a common ratio of 0.5: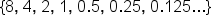

As the sequence continues, the values get smaller and smaller, getting closer and closer to zero.

In terms of the sum formula from above, this means that the numerator in the fraction actually simplifies to 1. So our formula for the sum of an infinite geometric sequence is simpler:

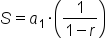formula to know

Sum of an Infinite Geometric Sequence

or

4. Using the Formula

EXAMPLE

Find the sum of the following infinite geometric sequence:

Our first task is to find the common ratio of the sequence. To do so, we can take two consecutive terms in the sequence and divide one by the other. It is important to divide the second number by the first, in order for the quotient to describe what must be multiplied by each term in the sequence to get the value of the following term:

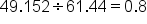Let's use 61.44 and 49.152, for instance. When we divide, we get , so 0.8 is the common ratio. You can test this out by multiplying each term by 0.8: 96 times 0.8 is 76.8, 76.8 times 0.8 is 61.44, etc.

Now we can use the formula for the sum of an infinite geometric sequence.

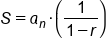
	Plug in
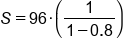
	Evaluate the denominator
	Evaluate the fraction
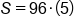
	Multiply
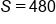
	Our solution

This means that the series will converge to 480. The sum will never exceed this value.