Table of Contents |
Before we introduce the FOIL method, it is helpful to review the distributive rule, because the two are similar processes. The distributive rule is used when a quantity is being multiplied by a sum.

EXAMPLE
 can be evaluated using distribution.
can be evaluated using distribution.

|
The 3 on the outside is multiplied into each term in the parentheses |
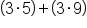
|
Find each sum |
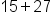
|
Evaluate |
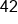
|
Our Solution |
 using the order of operations:
using the order of operations: 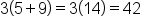 .
.
Earlier, we saw how distribution can help us evaluate expressions in the form 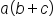 , by distributing
, by distributing 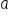 into
into 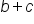 to get
to get 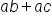 . How could we distribute something like
. How could we distribute something like  ?
?
We can evaluate such expressions through distribution, but the process works in a slightly different way. What really happens is that we distribute twice: first, we distribute 4 into 5 and 1, then we distribute 3 into 5 and 1. Take a look at how this distribution works:
EXAMPLE

|
Distribute 4 into 
|
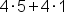
|
Distribute 3 into 
|

|
Evaluate and combine all parts |

|
Add |
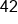
|
Our Solution |
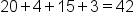 .
.
In short, we multiplied the first term in each factor, then the outside two terms, then the inside two terms, and then the last term in each factor. This is known as the FOIL method: First, Outside, Inside, Last.
Let's take a look at some more examples of using FOIL to evaluate expressions. As we work through these examples, pay attention to the sign of the numbers. We bring positive and negatives with us when distributing!
EXAMPLE

|
Distribute 5 into 
|

|
Distribute -2 into 
|
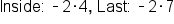
|
Combine all parts |

|
Change to subtraction |

|
Evaluate |

|
Our Solution |
EXAMPLE
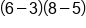
|
Distribute 6 into 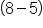
|
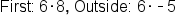
|
Distribute -3 into 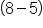
|
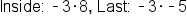
|
Combine all parts |

|
Change to subtraction |
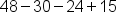
|
Evaluate |
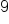
|
Our Solution |
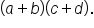 Remember, these are called binomials. If we're multiplying
Remember, these are called binomials. If we're multiplying  times
times 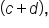 we are multiplying two binomials. When we practice using FOIL, the acronym can help us remember the steps for doing that distributing. It is important to remember that FOIL stands for First, Outer, Inner, and Last.
we are multiplying two binomials. When we practice using FOIL, the acronym can help us remember the steps for doing that distributing. It is important to remember that FOIL stands for First, Outer, Inner, and Last.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License