The Order of Operations

1. Importance of the Order of Operations

In math, an operation is a way to combine numbers, as in addition or subtraction. You can think of an operation in math as a calculation between two or more numbers.

There needs to be an agreed upon order for performing operations so that when there are several operations in an expression or an equation, everyone simplifies or solves in the same way to get the correct answer. Therefore, the order of operations is the rule that tells you the order in which to perform those operations.

The correct order of operations is Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction, otherwise referred to by the acronym PEMDAS.

You can use the order of operations to simplify an expression.

EXAMPLE

Suppose you want to simplify the expression: .

	Our Expression
	Start with division; divide 4 by 2.
	Next is addition and subtraction from left to right; first, add 10 and 2.
	Finish by subtracting 1 from 12.
	Our solution

Conversely, here is what happens if you simplify in the “wrong” order, moving simply from left to right and not using the order of operations. You would start with 10 plus 4, which equals 14. 14 divided by 2 is 7, and 7 minus 1 is 6, which is an incorrect answer.



Therefore, you can see that without having a standard order of operations, you can potentially arrive at two different answers.

big idea

The order of operations is used when performing all mathematical calculations, especially when solving equations and evaluating functions.

term to know

PEMDAS

An acronym used to remember the order of operations: parentheses, exponents, multiplication, division, addition, subtraction

2. PEMDAS

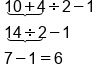
PEMDAS is the acronym you can use to remember the order of operations. PEMDAS stands for:

Parentheses
Exponents
Multiplication
Division
Addition
Subtraction

There are several important things to remember when using PEMDAS:

• Parentheses include other grouping symbols, such as brackets or radical signs.
• Multiplication and division are performed together from left to right in the order that they appear.
• Similarly, addition and subtraction are performed together from left to right in the order that they appear.

EXAMPLE

Suppose you want to simplify the following expression: .

	Our Expression
	Evaluate the equation inside of the parentheses; 7 minus 5 is 2.
	Next, we calculate the exponent; is 4.
	Now, we move onto multiplication; 3 times 2 is 6.
	Finally, addition and subtraction from left to right; 8-4 is 4.
	Add 4 and 6 to get 10.
	Our solution

hint

Note: the original expression had two sets of parentheses. The set of parentheses at the end of the expression (around the 2) are informing you that you multiply the 3 by the 2, an operation that will come later in the process.

The second example involves simplifying an expression containing negative numbers and exponents.

key concept

It is important to note a common mistake that people make when solving or simplifying expressions containing negative numbers and exponents. Consider the two similar, but different, equations or statements below:



In the first equation, you have negative 3 in parentheses squared, which equals a positive 9. Negative 3 squared means negative 3 times negative 3, which is a positive 9.



In the second equation, you have a negative 3 squared, which equals negative 9. That’s because the negative here is like a negative 1 being multiplied by the 3 squared. Therefore, the answer becomes negative 9.

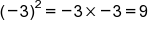
Now that you know how to avoid this common mistake, try using this knowledge when solving the equation in the second example.

EXAMPLE

Suppose you want to simplify the following expression: .

	Our Expression
	Evaluate the exponent; (the negative in front is like a negative 1 being multiplied, so you do not include it in your exponent operation).
	Next we move onto multiplication and division, moving from left to right; 12 divided by 2 is 6.
	Multiply 6 by 3, which is 18.
	Add negative 16 and 18.
	Our solution