Table of Contents |
Monomials are exponential expressions with non-negative integer exponents. There are three parts to a monomial: the base, the coefficient, and the exponent. The base is repeatedly multiplied by itself according to the exponent.
EXAMPLE
Consider the monomial shown below:
You can multiply monomials with and without coefficients.
EXAMPLE
Consider this expression without coefficients:
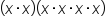

This illustrates the product property for exponential expressions, which works for the product of all monomials when the bases of the monomials are the same. In general, this states that 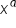 times
times  is equal to
is equal to  .
.
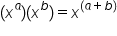
EXAMPLE
Consider the expression that involves multiplying monomials with coefficients:
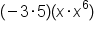

Exponents are generally integers or fractions, but they may be any number, such as a decimal. A rational exponent is an exponent that can be represented as a fraction.
The product property applies to all types of exponents, including integers and fractions. Therefore, you add fractions when applying the product property of exponents to rational exponents. You can easily add fractions when they have common denominators:
EXAMPLE
Suppose you want to simplify the following expression using the product property with rational exponents.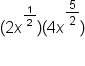
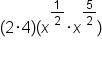

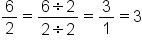

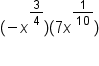
Source: This work is adapted from Sophia author Colleen Atakpu.