Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

The Quadratic Formula

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to solve a quadratic equation using the quadratic formula. Specifically, this lesson will cover:

Table of Contents

1. The Quadratic Formula

The quadratic formula is used to solve quadratic equations that are written in standard form 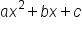a x squared plus b x plus c and set equal to zero. It uses the coefficients a comma b, and c that are found in the standard equation. The quadratic formula is:

formula to know
Quadratic Formula
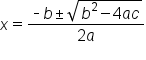
x equals fraction numerator short dash b plus-or-minus square root of b squared minus 4 a c end root over denominator 2 a end fraction

It looks like a complete mess, doesn't it? It can be a complicated formula to work through, but it is extremely useful in finding precise solutions to quadratic equations.

big idea
It is important to note that the quadratic equation must be in the form a x squared plus b x plus c equals 0.

2. When to Use the Quadratic Formula

As we saw in a previous lesson, one of the easiest ways to solve quadratic equations is to factor the expression and use the Zero Factor Property.

EXAMPLE

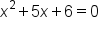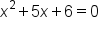
Find the solutions for the quadratic equation x squared plus 5 x plus 6 equals 0.

x squared plus 5 x plus 6 equals 0 Find two integers that multiply to 6 and add to 5
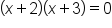
open parentheses x plus 2 close parentheses open parentheses x plus 3 close parentheses equals 0 Use the Zero Factor Property and set each factor equal to zero
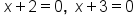
table row cell x plus 2 equals 0 comma end cell cell x plus 3 equals 0 end cell end table Evaluate
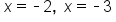
table row cell x equals short dash 2 comma end cell cell x equals short dash 3 end cell end table Our solutions

However, consider a more complicated quadratic equation where it cannot be solved easily with factoring:

EXAMPLE

Find the solutions for the quadratic equation x squared plus 4 x minus 10 equals 0.

We would need to find two numbers, p and q, that multiply to -10 and also add to 4. Looking at the factors of -10, we have:

p q sum: p + q
1 -10 -9
-1 10 9
2 -5 -3
-2 5 3

None of the pairs add up to 4, so this cannot be solved easily using factoring. We'll want to use a different method, such as the quadratic formula.

The quadratic expression in this example is known as a prime quadratic. Prime quadratics cannot be written in factored form, which means that factoring and solving using the Zero Factor Property is out of the question. In such cases, when we either cannot factor or are having trouble figuring out how to factor it, we can use the quadratic formula.

The quadratic formula can also tell us if there is a real solution to the quadratic equation. The expression underneath the radical is called the discriminant of the expression. Since it is underneath a square root, it must have a non-negative value to result in a real number.

  • If the discriminant is non-negative (zero or greater), the quadratic has at least one real solution
  • If the discriminant is negative (less than zero), the quadratic has no real solutions.

3. Solving Equations using the Quadratic Formula

When using the quadratic formula to solve a quadratic equation, use these steps:

step by step
  1. Set the equation equal to zero: a x squared plus b x plus c equals 0.
  2. Identify values for a comma b, and c.
  3. Plug these values into the quadratic formula.
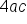  4. Simplify what is underneath the radical first: evaluate b squared and 4 a c, then find the difference. This is called the discriminant.
  5. Add the square root of the discriminant to -b and divide by 2 a. This is one solution for x.
  6. Subtract the square root of the discriminant from -b and divide by 2 a. This is the other solution for x.

Let's use the quadratic formula to solve the following equation:

EXAMPLE

Find the solutions to the quadratic equation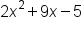 2 x squared plus 9 x minus 5.

At a quick glance, this doesn't seem like a quadratic that can be easily factored. Let's try using the quadratic formula instead.

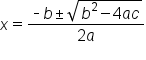
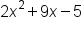
x equals fraction numerator short dash b plus-or-minus square root of b squared minus 4 a c end root over denominator 2 a end fraction Identify the values for a comma b, and c in the equation 2 x squared plus 9 x minus 5
a equals 2 comma space b equals 9 comma space c equals short dash 5 Substitute these values in the quadratic formula
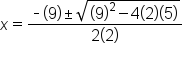
x equals fraction numerator short dash open parentheses 9 close parentheses plus-or-minus square root of open parentheses 9 close parentheses squared minus 4 open parentheses 2 close parentheses open parentheses 5 close parentheses end root over denominator 2 open parentheses 2 close parentheses end fraction In the discriminant, square 9 and multiply 4, 2, and -5
x equals fraction numerator short dash 9 plus-or-minus square root of 81 minus open parentheses short dash 40 close parentheses end root over denominator 2 open parentheses 2 close parentheses end fraction Find the difference in the discriminant
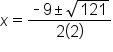
x equals fraction numerator short dash 9 plus-or-minus square root of 121 over denominator 2 open parentheses 2 close parentheses end fraction Evaluate the square root of 121
x equals fraction numerator short dash 9 plus-or-minus 11 over denominator 2 open parentheses 2 close parentheses end fraction Create two solutions, one with addition and one with subtraction
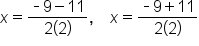
x equals fraction numerator short dash 9 minus 11 over denominator 2 open parentheses 2 close parentheses end fraction comma space space space space x equals fraction numerator short dash 9 plus 11 over denominator 2 open parentheses 2 close parentheses end fraction Evaluate
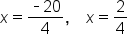
x equals fraction numerator short dash 20 over denominator 4 end fraction comma space space space space x equals 2 over 4 Simplify
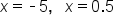
x equals short dash 5 comma space space space x equals 0.5 Our solutions

Let's look at a little more complicated problem.

EXAMPLE

Find the solutions to the quadratic equation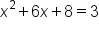 x squared plus 6 x plus 8 equals 3.

Don't jump the gun on identifying a comma b, and c to use in the quadratic formula. Remember, the equation needs to be set equal to zero before we begin to find solutions. Always be sure to check that your equation is set equal to zero. If it's not, we simply add or subtract terms from both sides of the equation, until zero is on one side of the equation, and everything else is on the other. For this specific equation, simply subtract 3 from both sides to get zero on the right side.

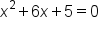
x squared plus 6 x plus 5 equals 0

Now we can use the quadratic formula and identify the variables a comma b, and c.

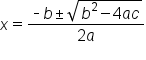
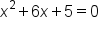
x equals fraction numerator short dash b plus-or-minus square root of b squared minus 4 a c end root over denominator 2 a end fraction Identify the values for a comma b, and c in the equation x squared plus 6 x plus 5 equals 0
a equals 1 comma space b equals 6 comma space c equals 5 Substitute these values in the quadratic formula
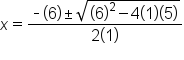
x equals fraction numerator short dash open parentheses 6 close parentheses plus-or-minus square root of open parentheses 6 close parentheses squared minus 4 open parentheses 1 close parentheses open parentheses 5 close parentheses end root over denominator 2 open parentheses 1 close parentheses end fraction In the discriminant, square 6 and multiply 4, 1, and 5
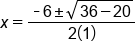
x equals fraction numerator short dash 6 plus-or-minus square root of 36 minus 20 end root over denominator 2 open parentheses 1 close parentheses end fraction Find the difference in the discriminant
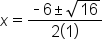
x equals fraction numerator short dash 6 plus-or-minus square root of 16 over denominator 2 open parentheses 1 close parentheses end fraction Evaluate the square root of 16
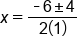
x equals fraction numerator short dash 6 plus-or-minus 4 over denominator 2 open parentheses 1 close parentheses end fraction Create two solutions, one with addition and one with subtraction
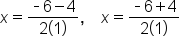
x equals fraction numerator short dash 6 minus 4 over denominator 2 open parentheses 1 close parentheses end fraction comma space space space space x equals fraction numerator short dash 6 plus 4 over denominator 2 open parentheses 1 close parentheses end fraction Evaluate
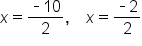
x equals fraction numerator short dash 10 over denominator 2 end fraction comma space space space space x equals fraction numerator short dash 2 over denominator 2 end fraction Simplify
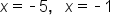
x equals short dash 5 comma space space space x equals short dash 1 Our solutions

summary
The quadratic formula is used to solve quadratic equations that are written in standard form and set equal to zero. It uses the coefficients a comma b, and c that are found in the standard equation. Prime quadratics cannot be factored because there are no two integers that will multiply to the constant term c and add to the b coefficient. Using the quadratic formula can be helpful in finding the solutions to x. When solving equations using the quadratic formula, the equation needs to be set equal to zero and then use the coefficients for a comma b, and c. 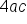If the value of the discriminant (b squared minus 4 a c) is negative, the equation has no real solution. If the value of the discriminant is non-negative, the equation has at least one real solution.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Quadratic Formula

x equals fraction numerator negative b plus-or-minus square root of b squared minus 4 a c end root over denominator 2 a end fraction

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.