Table of Contents |
Quadratic equations can be written in the form:

Factoring or variable isolation may be used to solve some, but not all, quadratic equations. However, the quadratic formula can be used to find solutions to all quadratic equations, even when factoring or variable isolation is difficult or impossible. Therefore, sometimes it’s necessary to use the quadratic formula to find solutions to a quadratic equation.
The quadratic formula states that for an equation in the form  , the solution(s) are:
, the solution(s) are:
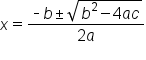
The values for a, b, and c in the formula come from the values of a, b, and c in the quadratic equation you want to solve. Notice that the equation must be set equal to 0 to get correct values for a, b, and c. When you use the quadratic formula, you often need to simplify square roots.
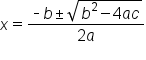
The following example illustrates a real-life application of solving a quadratic equation with a quadratic formula.
IN CONTEXT
Suppose Jason is competing in a shot-put event. How can you determine when the shot hit the ground? The height of the shot is modeled by the equation below, in which x is the time in seconds after the toss, and h of x is the vertical height of the shot.

Now, you want to find when the shot hit the ground, which means you want to know when the height is 0. Therefore, the equation you want to solve is the following:

You can solve this equation using the quadratic formula. Comparing your equation to the form of a standard quadratic equation, you can see that:Therefore, substituting these values into the formula gives you the expression:
- a = -16
- b = 20
- c = 6

Simplifying the denominator is an easy first step.

When you simplify the numerator, however, it’s more complicated because it involves a plus/minus symbol, square roots, and other operations. You’ll start to simplify underneath the square root and begin with your exponent,, then move on to the multiplication, then finally subtraction. Note that 784 is a perfect square, so you’ll finish by taking the square root.

You will need to separate your solution into two fractions.

It’s important to remember, though, that the plus and minus symbols gives you two solutions.

Simplifying these two fractions provides:

Add and subtract the fractions accordingly, then divide to provide your two solutions to this quadratic equation.

Going back to your original problem, you want to find the time it takes to reach the ground. Your solution of x equals -0.25 can be disregarded because it doesn’t make sense in the context of the problem. Therefore, it takes 1.5 seconds for the shot to hit the ground.
Source: This work is adapted from Sophia author Colleen Atakpu.