Table of Contents |
Recall that the area of a rectangle is found by multiplying the base times the height.
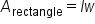
You can use this formula to solve real-world problems.
EXAMPLE
In the image below, we see a floor plan of an office space. In the office, there is the main section with workspaces and cubicles, a kitchenette, a break room, and a bathroom: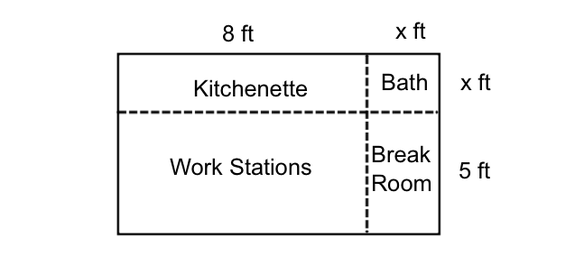
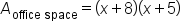
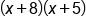
|
Multiply first terms: 
|

|
Multiply outside terms: 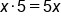
|
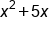
|
Multiply inside terms: 
|
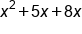
|
Multiply outside terms: 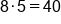
|
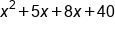
|
Expanded form |
 square feet
square feet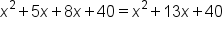
 .
.
We can also use the area equation to subtract space.
EXAMPLE
At a different office space, workers are coming in to install carpeting on the floor. However, they need to leave a border of wooden floors around the office for certain equipment. The floor plan is illustrated below: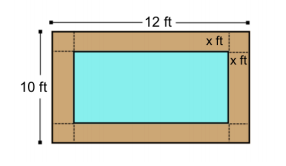
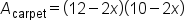

|
Multiply first terms: 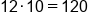
|

|
Multiply outside terms: 
|
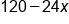
|
Multiply inside terms: 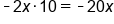
|
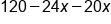
|
Multiply last terms: 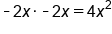
|
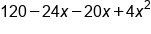
|
Combine like terms |
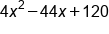
|
Our solution |
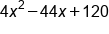 .
.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License