Using Linear Inequalities in Real World Scenarios

1. Linear Inequalities Representing a Budget/Cost Restraint

Many event planners and project managers that put on events have a certain budget they must stick to. This budget represents the maximum amount of dollars that you can spend on the event or project.

EXAMPLE

Suppose that you are an event planner with a certain budget planning a company's promotional event. One of the company's board members wants as many balloons at the party as possible. You would like to meet the client's desires, but you have already dedicated $1730 of your budget to other expenses. After researching the cost of balloons, you figure out that each balloon will cost about $1.30 in all - this factors in the purchase of each balloon and the helium for the tank.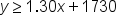

We can represent this scenario with the following inequality:

On one side of the inequality, we have a budget of y dollars. On the other side, we have our expression for the cost of the event: $1.30 per balloon plus $1730 in other costs. We can see that x represents the number of balloons. The inequality symbol we use is the "greater than or equal to" sign because we want our budget to remain greater than our cost (this means we'll have money to spare), but we are also allowed to spend exactly all of the money we have.

2. The Graph of a Linear Inequality

To graph the inequality for a situation, we need to analyze the inequality symbol. Inequality signs that include "or equal to" are drawn with a solid line on the graph, to show the inclusion of the exact values that the line graphs. If the symbol does not include "or equal to", then we use a dashed line to show that we are not accepted the exact values on the line as solutions to our inequality.

EXAMPLE

Graph the linear inequality for the scenario above.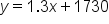

We start by drawing the boundary line, which is simply the equation . We also draw this as a solid line because the inequality has a "greater than or equal to" symbol.



Then we need to shade a region of the coordinate plane to highlight coordinate pairs that satisfy our inequality. We can use a test point to do so. Whenever possible, try choosing the origin (0, 0). This is because it is easy to multiply and add with zero when making calculations. If the test point satisfies the inequality, we shade the portion of the coordinate plan that includes the test point. If not, we shade the other portion of the coordinate plane.

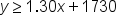
	Using the inequality, substitute 0 in for x and 0 in for y
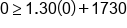
	Multiply 1.30 and 0
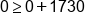
	Add 0 and 1730
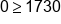
	False statement

When we tested the point (0, 0) with our inequality, we got a false statement because 0 is not greater than or equal to 1730. This tells us to shade the other part of the graph that does NOT include (0, 0).



We can call this region the solution region or feasibility region. Every coordinate point (x, y) in this solution region represents the maximum number of balloons we can spend, x, given that particular budget, y.

hint

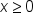In real-world scenarios, the inequalities and are often natural boundaries (we cannot buy negative balloons, and our budget cannot be negative dollars). This is why the negative sides of both x- and y-axis on the coordinate plane are not part of the solution region)

3. Using the Inequality and Graph to Solve Problems

You can then use a graph and an inequality to answer questions about a specific scenario. Let's continue using the information in the scenario from above to answer the following questions.

EXAMPLE

Can we afford to purchase 700 balloons for the event with a budget of $2500?

To answer this question, we plug 700 in for x and 2500 in for y. If the statement is true, we can afford 700 balloons with a budget of $2500.

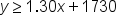
	Using the inequality, substitute 700 in for x and 2500 for y
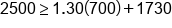
	Multiply 1.30 and 700
	Add 910 and 1730
	False statement

This means we cannot afford 700 balloons with a budget of $2500.

EXAMPLE

How many balloons can we purchase with a budget of $2000?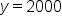

Let's first use the graph to get an estimate. We can add a horizontal line at and find where the line intersections the boundary line. This would represent the maximum number of balloons we can buy with a budget of $2000.



According to the graph, we estimate that we can buy no more than 200 balloons with our budget.

We can get an exact answer using the inequality and solving algebraically:

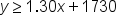
	Using the inequality, substitute 2000 in for y
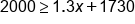
	Subtract 1730 from both sides
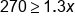
	Divide both sides by 1.3
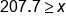
	Our solution

We can purchase 207 balloons. Let's investigate this answer further.

Because x represents the number of balloons, it doesn't make sense that our answer remains as a decimal (since you can't have a portion of a balloon). Therefore, we have to express our answer as a whole number. But in real-world scenarios, standard rounding rules might not make sense. In this example, we have to round 207.7 down to 207 rather than up to 208. If we had rounded to 208, we would be accepting 208 as an answer to the inequality, which would be false. 208 balloons would put the event cost at $2000.40, which is slightly over our budget.