Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Writing a Linear Equation Using Slope and Points

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to write a linear equation in slope-intercept form using a slope and a given point. Specifically, this lesson will cover:

Table of Contents

1. Forms of Linear Equations

When writing linear equations that rely on points on the line and the slopes of lines, we primarily work with two forms of linear equations: point-slope form, and slope-intercept form.

Equations written in slope-intercept form rely on the line's slope, m, and the y-coordinate of the y-intercept, b, to form the equation.

formula to know
Slope-Intercept Form
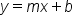
y equals m x plus b

Equations written in point-slope form rely on the line's slope, m, and a point on the line (x1, y1) to form the equation.

formula to know
Point-Slope Form
left parenthesis y minus y subscript 1 right parenthesis space equals space m left parenthesis x minus x subscript 1 right parenthesis

2. Using the Slope and a Point on the Line

When given information about a line's slope and a point on the line, it is easiest to write the equation in point-slope form, since the pertinent information needed to form the equation is already given to us.

EXAMPLE

Write the equation of a line with a slope of -2 that passes through the point (4, 9).

y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses Use the point-slope form and substitute the known values. First, replace m with the slope of -2
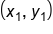y minus y subscript 1 equals short dash 2 open parentheses x minus x subscript 1 close parentheses Replace open parentheses x subscript 1 comma space y subscript 1 close parentheses with (4, 9)
y minus 9 equals short dash 2 open parentheses x minus 4 close parentheses Point-slope form

While developing the formula in point-slope form was certainly our easiest option, oftentimes having our equation in slope-intercept form is helpful so that we may graph the line. Slope-intercept form isolates y onto one side of the equation, with m x plus b on the other side of the equation. Let's see how we can take our equation in point-slope form, and rewrite it so that we can more easily graph this line:

EXAMPLE

Write the equation y minus 9 equals short dash 2 open parentheses x minus 4 close parentheses in slope-intercept form.

y minus 9 equals short dash 2 open parentheses x minus 4 close parentheses This equation is in point-slope form. Change to slope-intercept form by distributing -2
y minus 9 equals short dash 2 x plus 8 Add 9 to both sides
y equals short dash 2 x plus 17 Slope-intercept form

3. Using Two Points on the Line

When we are only given information about two points on the line, and no information about the slope of the line, we can use the same processes above, we just need to first calculate the line's slope ourselves. To do this, we use the following formula:

formula to know
Slope
m equals fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction

In the slope formula, recall that (x1, y1) and (x2, y2) are the two points on the line. In other words, we can find the difference in y-coordinates and divide it by the difference in x-coordinates to find the slope. This we can plug in to our equation for the line. From there, we can take any one of our two points to write the equation in point-slope form.

EXAMPLE

Find the equation of a line that passes through the points (-3, 2) and (1, 10) in both point-slope form and slope-intercept form.

First, we need to use the two points to calculate the slope:

m equals fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction Use the slope formula and substitute open parentheses x subscript 1 comma space y subscript 1 close parentheses equals open parentheses short dash 3 comma space 2 close parentheses and open parentheses x subscript 2 comma space y subscript 2 close parentheses equals open parentheses 1 comma space 10 close parentheses
m equals fraction numerator 10 minus 2 over denominator 1 minus open parentheses short dash 3 close parentheses end fraction Evaluate the numerator and denominator
m equals 8 over 4 Simplify
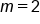
m equals 2 The slope

Now that we know the slope of the line, we can use either point to write the equation in point-slope form:

y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses Use the point-slope form and first substitute the slope 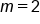m equals 2
y minus y subscript 1 equals 2 open parentheses x minus x subscript 1 close parentheses Substitute one of the points, for instance, open parentheses x subscript 1 comma space y subscript 1 close parentheses equals open parentheses short dash 3 comma space 2 close parentheses
y minus 2 equals 2 open parentheses x minus open parentheses short dash 3 close parentheses close parentheses Rewrite parentheses
y minus 2 equals 2 open parentheses x plus 3 close parentheses Point-slope form

Just like with our example before, we can rewrite this equation into slope-intercept form, so that we may more easily graph this line:

y minus 2 equals 2 open parentheses x plus 3 close parentheses Use the point-slope form and convert to slope-intercept by distributing the slope
y minus 2 equals 2 x plus 6 Add 2 to both sides
y equals 2 x plus 8 Slope-intercept form

4. Using Parallel and Perpendicular Lines

Sometimes we are given information about a line, and then asked to write the equation to a line parallel or perpendicular to it. In these cases, we need to apply the relationship between the slopes of parallel lines and the slopes between perpendicular lines.

  • Parallel lines have identical slopes. This means that the values for m in their equations is exactly the same.
  • Perpendicular lines have opposite reciprocal slopes. This means that not only is the slope "flipped" (the numerator becomes the denominator, and the denominator becomes the numerator), but the sign is reversed as well (positive becomes negative, and negative becomes positive).
It is probably more challenging to work with problems involving perpendicular lines, but we will go through examples of each:

EXAMPLE

Find the equation of the line perpendicular to y equals 4 over 3 x minus 6 that passes through the point (4, 2).

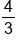For perpendicular lines, we know the slopes will opposite reciprocals. In the first line that was given, the slope is 4 over 3. For a line that is perpendicular, the slope will be 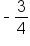short dash 3 over 4. We can now write an equation in point-slope form with m equals short dash 3 over 4 and open parentheses x subscript 1 comma space y subscript 1 close parentheses equals open parentheses 4 comma space 2 close parentheses.

y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses Use the point-slope form and substitute the known values: m equals short dash 3 over 4 and open parentheses x subscript 1 comma space y subscript 1 close parentheses equals open parentheses 4 comma space 2 close parentheses
y minus 2 equals short dash 3 over 4 open parentheses x minus 4 close parentheses Distribute the slope. Note that short dash 3 over 4 open parentheses short dash 4 close parentheses equals fraction numerator 3 over denominator up diagonal strike 4 end fraction times fraction numerator up diagonal strike 4 over denominator 1 end fraction equals 3
y minus 2 equals short dash 3 over 4 x plus 3 Add 2 to both sides
y equals short dash 3 over 4 x plus 5 Our Solution


The graph below shows the two perpendicular lines, y equals 4 over 3 x minus 6 and y equals short dash 3 over 4 x plus 5.

EXAMPLE

Find the equation of the line parallel to y equals 3 x plus 4 that passes through the point (1, -2) in slope-intercept form.

For parallel lines, we know that the slopes will be the same, so in this case, the slope will be 3. We can now write an equation in point-slope form with m equals 3 and open parentheses x subscript 1 comma space y subscript 1 close parentheses equals open parentheses 1 comma space short dash 2 close parentheses.

y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses Use the point-slope form and substitute the known values: m equals 3 and open parentheses x subscript 1 comma space y subscript 1 close parentheses equals open parentheses 1 comma space short dash 2 close parentheses
y minus open parentheses short dash 2 close parentheses equals 3 open parentheses x minus 1 close parentheses Rewrite left side
y plus 2 equals 3 open parentheses x minus 1 close parentheses Distribute the slope
y plus 2 equals 3 x minus 3 Subtract 2 from both sides
y equals 3 x minus 5 Our Solution


The graph below shows the two parallel lines, y equals 3 x plus 4 and y equals 3 x minus 5.

summary
Two different forms of linear equations are slope-point form and slope-intercept form. You can write an equation in slope-point form using the slope and a point on the line or using two points on the line. You can write an equation in slope-intercept form given certain information needed to determine the slope and y-intercept of the line. We can also write equations using parallel and perpendicular lines. Lines that are parallel to each other have the same slope. Lines that are perpendicular to each other have slopes that are opposite reciprocals.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Slope

m equals fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction

Slope-Intercept Form of a Line

y equals m x plus b

Slope-Point Form of a Line

y minus y subscript 1 equals m left parenthesis x minus x subscript 1 right parenthesis

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.