Table of Contents |
Writing a linear inequality from a graph is similar to writing a linear equation from a graph. The biggest difference is that with inequalities, a portion of the coordinate plane is highlighted to represent the solution region. Another thing to consider is how the line is drawn: whether a solid or a dashed line is used. These two characteristics, the highlighted solution region and the type of line drawn, will help us determine what inequality symbol to use when writing the inequality.
First, we'll start with determining the other parts of the inequality. To do this, we will somewhat ignore the fact that we're dealing with an inequality, at least for now, and focus on the boundary line to write an equation in the form 
EXAMPLE
Write the inequality that corresponds to the graph below:
 , because there is a rise of -1 for every run of 3 to get from one point to the next.
, because there is a rise of -1 for every run of 3 to get from one point to the next.


If a boundary line is a vertical line, this can be presented by the equation  . The inequality that we will write to represent this graph has no y-component at all. This simply highlights all x-values on one side of the boundary line, no matter what the value of y is.
. The inequality that we will write to represent this graph has no y-component at all. This simply highlights all x-values on one side of the boundary line, no matter what the value of y is.
Once again, we look at the type of line used in the graph to determine if our inequality symbol will be strict or non-strict. However, we interpret "above the line" or "below the line" a bit differently. Think about the values of x that run along the x-axis. As we read the graph from left to right, our x-values go from negative infinity to positive infinity. Thus, "above the line" should be interpreted as "to the right" and "below the line" should be interpreted as "to the left."
EXAMPLE
Write the inequality that corresponds to the graph below:
 , and the area to the right of the boundary line is shaded as the solution region. This means that our inequality symbol will indicate values greater than 3, but not including 3 (because of the dashed line). Thus, our inequality is:
, and the area to the right of the boundary line is shaded as the solution region. This means that our inequality symbol will indicate values greater than 3, but not including 3 (because of the dashed line). Thus, our inequality is:

If a boundary line is a horizontal line, this can be presented by the equation  . In contrast to our vertical boundary lines, this has no x-component in the equation or inequality. This means that all values either greater than or less than a certain value for y are in the solution region, no matter what the value of x is.
. In contrast to our vertical boundary lines, this has no x-component in the equation or inequality. This means that all values either greater than or less than a certain value for y are in the solution region, no matter what the value of x is.
EXAMPLE
Write the inequality that corresponds to the graph below:
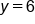 . Now, we just need to determine an inequality symbol.
. Now, we just need to determine an inequality symbol.
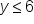
 where
where  is the value on the x-axis that the line crosses. A horizontal boundary line is represented with the equation y equals
is the value on the x-axis that the line crosses. A horizontal boundary line is represented with the equation y equals  where
where  is the value on the y-axis that the line crosses.
is the value on the y-axis that the line crosses.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License