Table of Contents |
Before we begin to write equations from a graph, let's review some important information about the graphs of lines: slopes and intercepts. Being able to easily identify slopes and intercepts from a graph will be extremely useful when writing the equation to the line.
The slope of a line can be found by using any two points on a graph. All we need are the x- and y-coordinates from two points to plug into our equation for slope:

Intercepts are where the line crosses a particular axis.
 , and at the y-intercept,
, and at the y-intercept, 
If the y-intercept of a line is displayed on the graph, we will want to write the equation in slope-intercept form, because part of the equation contains the y-intercept itself, or at least the y-coordinate of it. Slope-intercept form is 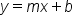 , where b is the y-coordinate of the y-intercept. The only other thing we will need to solve for is the slope.
, where b is the y-coordinate of the y-intercept. The only other thing we will need to solve for is the slope.
EXAMPLE
Find the equation of the line graphed below:

|
Use the slope formula and substitute in the two points:  and and 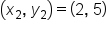
|
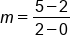
|
Evaluate the numerator and denominator |

|
The slope |
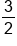 , and the y-coordinate of the y-intercept, 2, we can write the equation of the line in slope-intercept form:
, and the y-coordinate of the y-intercept, 2, we can write the equation of the line in slope-intercept form:
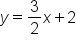
In our first example, we saw how helpful it was to use the y-intercept on the graph to design our equation. Sometimes, the y-intercept is not visible on the graph, but we can calculate it algebraically. The first thing we'll want to do in this situation is locate any two points on the graph and calculate the slope. From there, we will be able to plug in fixed values for everything else in slope-intercept form, thus allowing us to solve for b.
EXAMPLE
Write the equation to the line graphed below:

|
Use the slope formula and substitute in the two points: 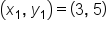 and and 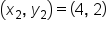
|

|
Evaluate the numerator and denominator |

|
Simplify |
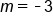
|
The slope |
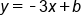 . We just need to solve for b. To do this, we can take any point on the line, plug in the coordinates of that point for x and y in the equation, and solve for b. To make things easier, we can choose either of the two points we have already identified when we calculated the slope. Let's use the point (4, 2). This means that we will plug in 4 for x and 2 for y in the equation
. We just need to solve for b. To do this, we can take any point on the line, plug in the coordinates of that point for x and y in the equation, and solve for b. To make things easier, we can choose either of the two points we have already identified when we calculated the slope. Let's use the point (4, 2). This means that we will plug in 4 for x and 2 for y in the equation 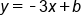 .
.
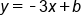
|
Using the equation that we have so far, plug in a point on the line, for instance, (4, 2). Substitute 4 for x and 2 for y |
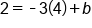
|
Multiply -3 and 4 |
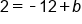
|
Add 12 to both sides |
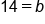
|
The y-coordinate of the y-intercept |
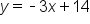 .
.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License