Writing Equivalent Equations

1. Equivalent Equations

In mathematics, we work with equivalent equations all the time. Think about the process for solving a multi-step equation. We might start with something such as . Using inverse operations, we create a series of equivalent equations in order to find a value for x.

	Subtract 3 from both sides
	This is considered an equivalent equation. Divide both sides by 4 to get another equivalent equation.
	A second equivalent equation

The equations above are all considered equivalent equations, because they have the same solution. In each equation, the solution is

2. Determining if Two Equations are Equivalent

In order to determine if two equations are equivalent, we will solve each equation, and then compare their solutions. If their solutions are the same, we can say the equations are equivalent. If the solutions are not the same, we know that the equations are not equivalent.

EXAMPLE

Determine if the equations below are equivalent: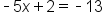

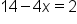
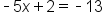
Solve each equation separately:

	Subtract 2 from both sides
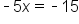
	Divide both sides by -5
	Our Solution

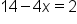
	Subtract 14 from both sides
	Divide both sides by -4
	Our Solution

The solutions to our equations are both and . Since the solutions are the same, the two equations are equivalent.

EXAMPLE

Determine if the equations below are equivalent: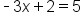

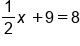
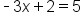
Solve each equation separately:

	Subtract 2 from both sides
	Divide both sides by -3
	Our Solution

	Subtract 9 from both sides
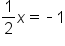
	Multiply both sides by 2
	Our Solution

The solutions to our equations are and Since the solutions are not the same, the two equations are not equivalent.