Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Add and Subtract Complex Numbers

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to add or subtract two complex numbers. Specifically, this lesson will cover:

Table of Contents

1. Complex Numbers

A complex number is a number in the form a plus b i, containing both a real and imaginary part. The imaginary part is followed by i, which is the imaginary unit, square root of short dash 1 end root.

Recall the following formulas for imaginary numbers:

formula to know
Imaginary Number
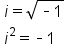
table attributes columnalign left end attributes row cell i equals square root of short dash 1 end root end cell row cell i squared equals short dash 1 end cell end table

We can combine complex numbers through addition and subtraction, just like we can add or subtract real numbers. The biggest distinction is that the real numbers and imaginary numbers remain separated, as is the case when combining like terms. This is the case with both addition and subtraction, where the only difference in the processes is the operation.

2. Adding Complex Numbers

We can think of a complex number addition problem as containing two addition sets. First, we'll add the real numbers together, which will constitute the first half of our solution. Secondly, we'll add the imaginary numbers together, and express that as the second half of the solution.

EXAMPLE

Add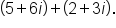 open parentheses 5 plus 6 i close parentheses plus open parentheses 2 plus 3 i close parentheses.

Start by lining up the two expressions. Add the real numbers together and then add the imaginary numbers together.

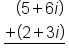
table attributes columnalign left end attributes row cell space space space open parentheses 5 plus 6 i close parentheses end cell row cell stack plus open parentheses 2 plus 3 i close parentheses with bar below end cell end table Add real numbers, 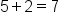5 plus 2 equals 7
7 space space space space space space space space Add imaginary numbers, 6 i plus 3 i equals 9 i
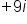
plus 9 i Combine both parts
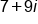
7 plus 9 i Our solution

Sometimes, the addition of the two complex numbers has negative numbers in them. In these cases, we follow the same process when adding negative numbers: we can think of adding a negative number as subtracting a positive number.

EXAMPLE

Add open parentheses short dash 3 plus 4 i close parentheses plus open parentheses 5 minus 7 i close parentheses.

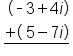
table attributes columnalign left end attributes row cell space open parentheses short dash 3 plus 4 i close parentheses end cell row cell stack plus open parentheses space 5 minus 7 i close parentheses with bar below end cell end table Add real numbers, short dash 3 plus 5 equals 2
2 space space space space space space space space Add imaginary numbers, 4 i plus open parentheses short dash 7 i close parentheses equals short dash 3 i
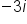
negative 3 i Combine both parts
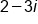
2 minus 3 i Our solution

3. Subtracting Complex Numbers

When subtracting complex numbers, we again can break the problem down into two sets of subtraction: one set for all real numbers, and another set for imaginary numbers. The trickiest part with subtraction problems is paying attention to the sign of the numbers and the differences. This will be a particular concern when the subtraction problem contains negative numbers. Below are some examples of complex number subtraction:

EXAMPLE

Subtract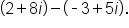 open parentheses 2 plus 8 i close parentheses minus open parentheses short dash 3 plus 5 i close parentheses.

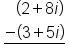
table attributes columnalign left end attributes row cell space space space open parentheses 2 plus 8 i close parentheses end cell row cell stack negative open parentheses 3 plus 5 i close parentheses with bar below end cell end table Subtract real numbers, 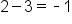2 minus 3 equals short dash 1
short dash 1 space space space space space space space space Subtract imaginary numbers, 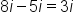8 i minus 5 i equals 3 i
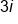
3 i space Combine both parts
short dash 1 plus 3 i Our solution

hint
Be sure to still combine the real number and the imaginary number with addition. Although we are performing subtraction, remember that our general complex number is in the form a plus b i. We would only see a minus sign between the two terms if the imaginary part was negative.

EXAMPLE

Subtract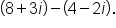 open parentheses 8 plus 3 i close parentheses minus open parentheses 4 minus 2 i close parentheses.

table attributes columnalign left end attributes row cell space space space space open parentheses 8 plus 3 i close parentheses end cell row cell stack negative space open parentheses 4 minus 2 i close parentheses with bar below end cell end table Subtract real numbers, 8 minus 4 equals 4
4 space space space space space space space space Subtract imaginary numbers, 3 i minus open parentheses short dash 2 i close parentheses equals 5 i
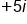
plus 5 i Combine both parts
4 plus 5 i Our solution

hint
There is one thing, in particular, to note in the previous example. When subtracting the imaginary numbers, we subtracted a negative number, where we had 3i minus negative 2i. This can be thought of as adding a positive number, or 3i plus positive 2i.

summary
Complex numbers consist of a real part and an imaginary part. The square root of negative 1 is imaginary because no real number squared results in a negative number. When adding or subtracting complex numbers, you first combine the real numbers, and then combine the imaginary numbers.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Imaginary Number

i equals square root of short dash 1 end root i squared equals short dash 1


© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.