Table of Contents |
The first type of a compound inequality is an "OR" inequality. For this type of inequality we want a true statement from either one inequality OR the other inequality OR both. When we are graphing these type of inequalities we will graph each individual inequality above the number line, then move them both down together onto the actual number line for our graph that combines them together.
When we give interval notation for our solution, if there are two different parts to the graph we will put a ∪ (union) symbol between two sets of interval notation, one for each part.
EXAMPLE
Suppose the value of x falls under or
or  . Solve each inequality, graph the solution, and give interval notation of the solution.
. Solve each inequality, graph the solution, and give interval notation of the solution.
 
|
Solve by first adding 5 to both sides. |
 
|
Divide both sides by 2 |

|
Our solution |
 
|
Solve by first subtracting 4 from both sides. |
 
|
Divide both sides by -1. Don't forget to flip the sign! |

|
Our solution |


There are several different results that could result from an "OR" statement. The graphs could be pointing in different directions with no overlap (like in the example above), pointing in the same direction, or pointing in opposite directions with an overlap. In the table below, notice how interval notation works for each of these cases.
| "OR" Inequalities | ||
| Type | Example | Directions |
|---|---|---|
| Arrows pointing in opposite directions with NO overlap |
 Interval Notation: 
|
In this graph, both graphs can be true for the inequality. |
| Arrows point in same directions |
 Interval Notation: 
|
As the graphs overlap, we take the largest graph for our solution. |
| Arrows point in opposite directions and do overlap |
 Interval Notation: 
|
When the graphs are combined, they cover the entire number line. |
The second type of compound inequality is an "AND" inequality. "AND" inequalities require both statements to be true. If one is false, they both are false. When we graph these inequalities we can follow a similar process, first graph both inequalities above the number line, but this time only where they overlap will be drawn onto the number line for our final graph. When our solution is given in interval notation it will be expressed in a manner very similar to single inequalities (there is a symbol that can be used for "AND", the intersection, ∩ , but we will not use it here).
EXAMPLE
Suppose the value of x falls under and
and  . Solve each inequality, graph the solution, and give interval notation of the solution.
. Solve each inequality, graph the solution, and give interval notation of the solution.

|
Solve by first adding 7 to both sides. |

|
Divide both sides by 3 |

|
Rewrite with x on the left side |

|
Our solution |
 
|
Solve by first subtracting 3x from both sides. |
 
|
Divide both sides by 2 |
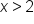
|
Our solution |


Again, as we graph "AND" inequalities, only the overlapping parts of the individual graphs makes it to the final number line. As we graph "AND" inequalities, there are three different types of results we could get. The first is from in the above example.
| "AND" Inequalities | ||
| Type | Example | Directions |
|---|---|---|
| Arrows pointing in opposite directions and overlap |
 Interval Notation: 
|
In this graph, only the overlapping parts of the individual graphs makes it to the final number line. |
| Arrows point in same directions |
 Interval Notation: 
|
In this graph, the overlap is only the smaller graph, so this is what makes it to the final number line. |
| Arrows point in opposite directions and do NOT overlap |
 Interval Notation: No Solution or 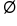
|
In this graph, there is no overlap of the parts. Because of this, no value makes it to the final number line |
The third type of compound inequality is a special type of "AND" inequality. When our variable (or expression containing the variable) is between two numbers, we can write it as a single math sentence with three parts, such as 5 less than x less or equal than 8, to show x is between 5 and 8 (or equal to 8). When solving these type of inequalities, because there are three parts to work with, to stay balanced we will do the same thing to all three parts (rather than just both sides) to isolate the variable in the middle. The graph then is simply the values between the numbers with appropriate brackets on the ends.
EXAMPLE
Suppose the value of x falls under . Solve the inequality, graph the solution, and give interval notation of the solution.
. Solve the inequality, graph the solution, and give interval notation of the solution.
 
|
Subtract 2 from all three parts |
 
|
Divide all three parts by  . Don't forget to flip the symbols! . Don't forget to flip the symbols!
|

|
Flip entire statement so values get larger left to right |

|
Our solution |


Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License