Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Continuously Compounding Interest

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to solve for account balance when interest is compounded continuously. Specifically, this lesson will cover:

Table of Contents

1. Compound Interest

Bank and investment accounts appreciate in value according to compounding interest. For many, the account has an annual percentage rate (APR) that is compounded periodically throughout the year. This means that a portion of the APR is applied each time the interest is compounded.

EXAMPLE

If interest is compounded quarterly, one-fourth of the interest is applied each quarter, for a total of four times per year.

We can represent compounding interest using the following formula:

formula to know
Compound Interest
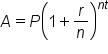
A equals P open parentheses 1 plus r over n close parentheses to the power of n t end exponent

In this formula,

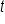  • A is the account balance after t number of years.
  • P is the principal (initial starting balance).
  • r is the annual percentage rate (expressed as a decimal).
  • n is the number of times per year interest is compounded.
  • t is time in years.

2. Continuously Compounding Interest

When interest is compounding continuously, we can think of the variable n (the number of times per year interest is compounded) as being infinitely large. How do we make sense of our formula if n is an infinitely large number? Let's isolate the part of our formula that relies on the variable n, and consider when n approaches infinity:

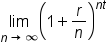
limit as n rightwards arrow infinity of open parentheses 1 plus r over n close parentheses to the power of n t end exponent

hint
For these purposes, it isn't so important that we understand this notation, but this denotes the limit of the expression as n approaches infinity. The limit represents a value that the expression approaches, but will not exceed.

As it turns out, as n gets infinitely larger, the expression 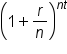open parentheses 1 plus r over n close parentheses to the power of n t end exponent simplifies to 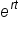e to the power of r t end exponent. Recall that 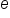e is a mathematical constant, approximately equal to 2.718282. Having this in mind, we can adjust our interest formula for continuously compounding interest:

formula to know
Continuously Compounding Interest
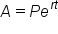
A equals P e to the power of r t end exponent

In this formula,

  • A is the account balance after t number of years
  • P is the principal (initial starting balance)
  • e is the mathematical constant, approximately equal to 2.718282
  • r is the annual percentage rate (expressed as a decimal)
  • t is time in years

3. Solving for Account Balance

Now that we have a formula to use when interest is compounded continuously, let's use it to solve some problems with account balances.

EXAMPLE

An account has an initial balance of $1150.00 and has an APR of 2%, which is compounded continuously. What is the balance of the account after 3 years, assuming no additional deposits or withdrawals are made?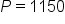

Let's identify values we can plug in for the variables in our formula:
  • P equals 1150
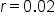
  • r equals 0.02
  • t equals 3
We can plug these into the variables in our continuously compounded interest formula:

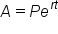
A equals P e to the power of r t end exponent Plug in P equals 1150 comma space r equals 0.02 comma space t equals 3
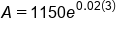
A equals 1150 e to the power of 0.02 open parentheses 3 close parentheses end exponent Evaluate multiplication in exponent
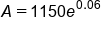
A equals 1150 e to the power of 0.06 end exponent Apply exponent to e
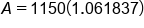
A equals 1150 open parentheses 1.061837 close parentheses Multiply by principal balance
A equals 1221.11 Our solution

The account balance will be $1,221.11 after 3 years.

hint
If your calculator has the e button, use it to get the most accurate answer. If not, use the approximation 2.718282 and use as many decimal digits as possible during your calculations, and round to the nearest cent at the very end only. If you round too often during the calculations, you may get the same dollar amount, but the cents will likely be off.

4. Solving for Growth Time

We can also use the formula for continuously compounding interest to solve for the time it takes for the account to reach a certain value.

EXAMPLE

A savings account has a balance of $4,500. The interest rate of the account is 3.5% annually, which is compounded continuously. How long will take for the account to reach a value of $7,000, assuming no additional deposits or withdrawals are made?

Again, let's match up given information with variables in our formula:
  • P equals 4500
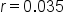
  • r equals 0.035
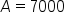
  • A equals 7000
Here, we want to solve for t, so this remains our unknown. The equation for this situation is:

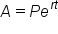
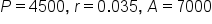
A equals P e to the power of r t end exponent Plug in P equals 4500 comma space r equals 0.035 comma space A equals 7000
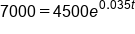
7000 equals 4500 e to the power of 0.035 t end exponent Solve for t

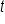How can we solve for the variable t? One thing to note right away is that the variable t is an exponent here. The exponent 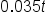0.035 t is applied only to the mathematical constant e, not the principal balance, P. So our first step should always be to divide both sides of the equation by the principal.

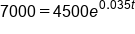
7000 equals 4500 e to the power of 0.035 t end exponent Divide by 4500
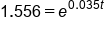
1.556 equals e to the power of 0.035 t end exponent Solve for t

Now we are ready to undo the exponent in order to isolate t. This requires applying a logarithm to undo the exponent. The important thing here is to consider the base of the log. Since the base of the exponential is e, we should use the natural log to solve for t.

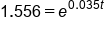
1.556 equals e to the power of 0.035 t end exponent Take the natural log of both sides
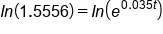
I n open parentheses 1.5556 close parentheses equals I n open parentheses e to the power of 0.035 t end exponent close parentheses Appy the Power Property of Logs
I n open parentheses 1.5556 close parentheses equals 0.035 t times I n open parentheses e close parentheses Simplify the left side with 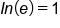I n open parentheses e close parentheses equals 1
I n open parentheses 1.5556 close parentheses equals 0.035 t Divide both sides by 0.035
fraction numerator I n open parentheses 1.5556 close parentheses over denominator 0.035 end fraction equals t Evaluate fraction
12.62 equals t Our solution
12.62 space y e a r s Our solution

It will take 12.62 years for the account to reach a value of $7,000.

hint
Notice the relationship between e and the natural log, ln. The natural log is the inverse of e. So when you take the natural log of e, or ln open parentheses e close parentheses, this is simply equal to 1.

summary
Bank and investment accounts appreciate in value according to compound interest. Some bank accounts gain interest continuously. With continuously compounding interest, n, the number of times interest is compounded per year, is an infinitely large number. The continuously compounded interest formula uses the mathematical constant e, which is equal to approximately 2.718281. When solving for account balance, you will solve for A. For solving for growth time, you will solve for t using logarithms.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Compound Interest

A equals P open parentheses 1 plus r over n close parentheses to the power of n t end exponent

Continuously Compounding Interest

A equals P e to the power of r t end exponent

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.