Table of Contents |
Linear equations can be written in several different forms. Sometimes, it is beneficial to have the equation to the same line written in a different form, so that you can more readily draw certain information about the line just by looking at its equation. For instance, having an equation written in standard form doesn't make it easy to identify the line's slope, or at least not as easy as the same line written in slope-intercept form or point-slope form. Likewise, if an equation is written in slope-point form, and you wish to easily identify the line's y-intercept, converting the equation into the slope-intercept form will be helpful.
In this tutorial, we are going to go through a few examples of converting from one form to another, in order to more easily draw conclusions about a line's slope, intercept, or point on the line. Here are the forms again as a review:
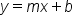
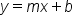

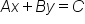
When you need to find the slope and intercept of an equation, it is best to convert the equation into slope-intercept form (if it is not already in that form).
EXAMPLE
Find the slope and intercept for the equation
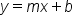 , so we can simply look at m and b for that information. As you read the steps below, keep in mind that the overall goal is to get the y-term by itself on one side of the equation, and then cancel the coefficient in front of y.
, so we can simply look at m and b for that information. As you read the steps below, keep in mind that the overall goal is to get the y-term by itself on one side of the equation, and then cancel the coefficient in front of y.

|
This equation is currently in standard form. Convert to slope-intercept form by first subtracting 2x from both sides |
|
Divide all terms by -3 (note the x-term coefficient will now be positive) |
|
Rearrange to 
|

|
Slope-Intercept Form |
While both point-slope form and slope-intercept form provide information about a line's slope, and technically a point on the line as well, point-slope form can give the location to any point on the line, whereas slope-intercept form gives only the y-coordinate to the y-intercept.
EXAMPLE
Suppose a line has a slope of 4 and passes through the point (-3, 7). What is the line's y-intercept?

|
This is the point-slope form equation. Substitute the known values:  , , 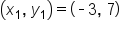 
|

|
Distribute 4 into (x + 3) |

|
Add 7 to both sides |
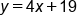
|
Use this to find the y-intercept |
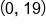
|
y-intercept |
Having an equation in standard form can help us easily calculate both x- and y-intercepts. This is because for each intercept, either x or y will be zero, making the entire x or y term in the equation equal to zero. In this final example, we are going to covert an equation from slope-intercept form into standard form, and then identify both x- and y-intercepts using the equation in standard form:
EXAMPLE
Convert the equation into standard form and identify the x-intercept and y-intercept.
into standard form and identify the x-intercept and y-intercept.

|
This equation is currently in slope-intercept form. Convert to standard form by first moving the x-term to the same side as the y-term. Subtract 2x from both sides |
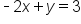
|
Multiply everything by -1, since the coefficient of x should not be negative |

|
Standard form |

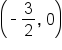 .
.
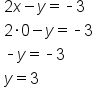
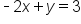 to
to  . This is because we prefer the x-term to have a positive coefficient, so in these cases, the signs of all terms must switch.
. This is because we prefer the x-term to have a positive coefficient, so in these cases, the signs of all terms must switch.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License