Finding the Inverse of a Function

1. Inverse Functions

An inverse function undoes the operations performed on variables of a function.

EXAMPLE

If a number is multiplied by 2, and added by 3, we can write this as the function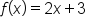 . The inverse to this function first subtracts 3 from the input value, and then divides by 2, so as to completely undo all operations of the original function. We write this as the inverse function .

big idea

If a function becomes the input of an inverse function, then the output is the argument of the original function. Mathematically, we write this as:

2. Evaluating an Inverse Graphically

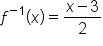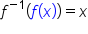
On a graph, the x- and y-coordinates between a function and its inverse are inverted or swapped. This means that for any coordinate, (x, y), of a function, we can find a corresponding coordinate on the graph of its inverse using the coordinates (y, x). This means we locate the x-value on the y-axis, and locate the y-value on the x-axis.

EXAMPLE

Check out the graph of a function and its inverse.

Points on	Points on
(2, 7)	(7, 2)
(-2, -1)	(-1, -2)

3. Finding the Inverse Algebraically

If we want to find the inverse of a function algebraically, there are two common procedures most people use:

1. Rewrite the equation, except swap x and y. Then, rewrite the equation so that y is isolated on one side of the equation.
2. Do the same process, but in reverse order. First, you can rewrite the equation so that x is isolated on one side of the equation. Then, simply swap x and y. The resulting equation will be the defined inverse function.

EXAMPLE

Find the inverse of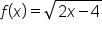 using the first method where we swap x and y.

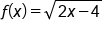
	Rewrite the function as
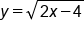
	Swap x and y
	Square both sides
	Add 4 to both sides
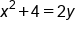
	Divide both sides by 2
	Our solution for y
	Our solution in inverse notation

EXAMPLE

Find the inverse of .

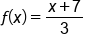
	Rewrite the function as
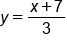
	Swap x and y
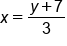
	Multiply both sides by 3
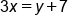
	Subtract 7 from both sides
	Our solution for y
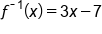
	Our solution in inverse notation

hint

Technically, we need to restrict the domain of the inverse function to non-negative values of x. This is because the range of the original function was restricted to non-negative y-values. The domain and range of a function also swap when defining the domain and range of its inverse.

summary

The inverse of a function undoes the operations of the function. We can evaluate an inverse graphically by comparing the coordinate points. All points on the curve of can be described as (x, y). All points on the curve inverse of can be described as (y, x), where x and y are the coordinates of the original function. The inverse can be found algebraically by swapping x and y, and then solving the equation for y.