Table of Contents |
So far in this course, we have only talked about equalities; in other words,  or
or  . In this lesson, we will cover inequalities. An inequality is a mathematical statement to show that one quantity is greater than or less than another quantity. The following outlines the different inequality symbols and their meanings:
. In this lesson, we will cover inequalities. An inequality is a mathematical statement to show that one quantity is greater than or less than another quantity. The following outlines the different inequality symbols and their meanings:
| Symbol | Translation | Example |
|---|---|---|
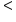
|
Less than |
3 < 5 3 is less than 5 |
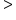
|
Greater than |
7 > 5 7 is greater than 5 |
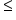
|
Less than or equal to |
4 ≤ 5 4 is less than or equal to 5 |
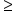
|
Greater than or equal to |
8 ≥ 5 8 is greater than or equal to five |
EXAMPLE
If we have an expression such as , this means our variable can be any number smaller than 4 such as -2, 0, 3, 3.9, or even 3.999999999, just as long as it is smaller than 4.
, this means our variable can be any number smaller than 4 such as -2, 0, 3, 3.9, or even 3.999999999, just as long as it is smaller than 4.
EXAMPLE
If we have an expression such as , this means our variable can be any number greater than or equal to -2, such as 5, 0, -1, -1.9999, or even -2.
, this means our variable can be any number greater than or equal to -2, such as 5, 0, -1, -1.9999, or even -2.
Because we don’t have one set value for our variable, it is often useful to draw a picture of the solutions to the inequality on a number line. On a number line, we define specific intervals on the number line using symbols. An endpoint is where a range of values starts or ends.
EXAMPLE
Let’s look at the interval on the number line below. Here is our number line with a highlighted range of values: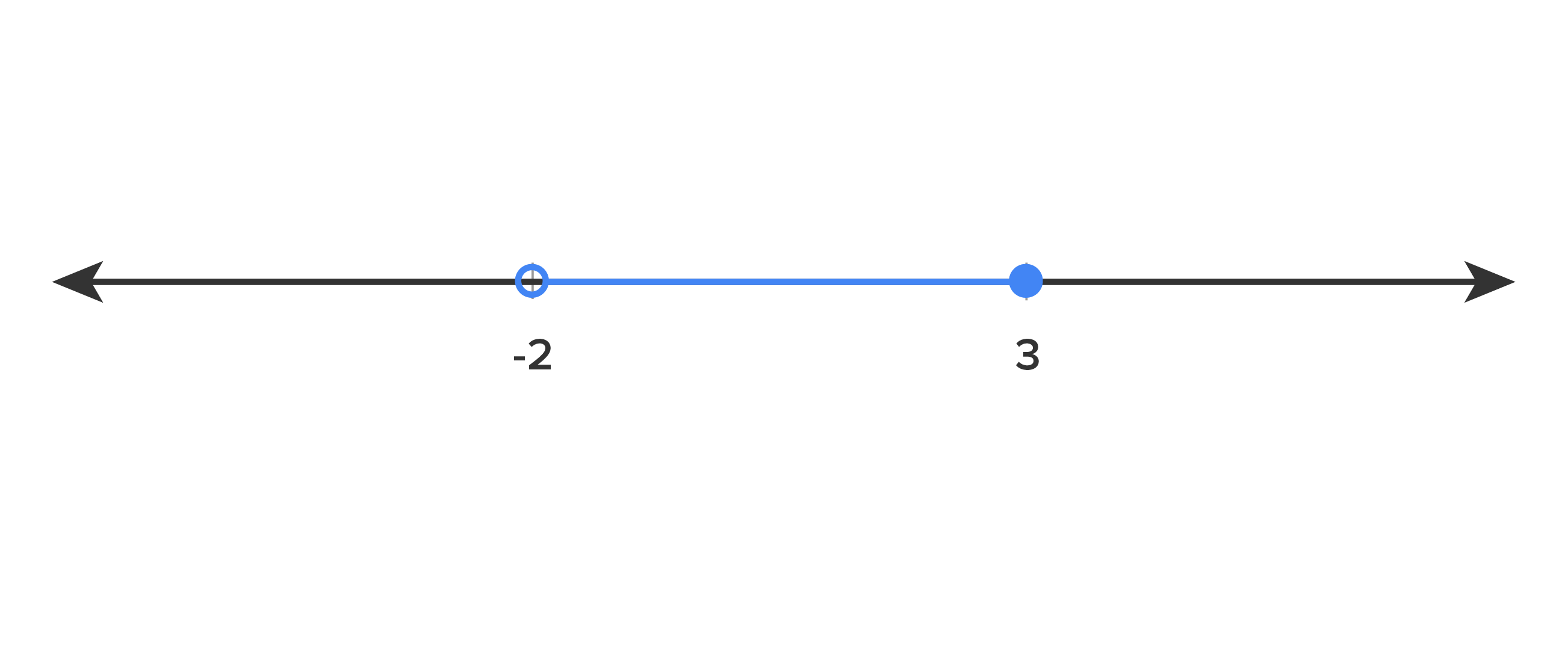
In general, we will use open and close circles to indicate endpoints:
| Open and Closed Circles for Intervals on a Number Line | |
| Endpoint is Included in Interval | Endpoint is Not Included in Interval |
|---|---|

|

|
EXAMPLE
Graph the inequality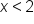 .
.
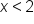 , we know that x cannot be exactly equal to 2, but can be anything smaller. First, we show that x cannot be exactly equal to 2 by putting an open circle on the number line right at 2. An open circle means that the value for x cannot be exactly equal to the value that it's on top of. We also want to show that x can be any value less than 2. We can use an arrow pointing to the left, or pointing to the numbers that are less than 2. The region in the image represents all the solutions to the inequality, x is less than 2, and any value in the highlighted region is going to satisfy this inequality.
, we know that x cannot be exactly equal to 2, but can be anything smaller. First, we show that x cannot be exactly equal to 2 by putting an open circle on the number line right at 2. An open circle means that the value for x cannot be exactly equal to the value that it's on top of. We also want to show that x can be any value less than 2. We can use an arrow pointing to the left, or pointing to the numbers that are less than 2. The region in the image represents all the solutions to the inequality, x is less than 2, and any value in the highlighted region is going to satisfy this inequality.

EXAMPLE
Graph the inequality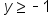 .
.
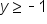 . Any value of y in this highlighted region, including -1, is going to satisfy the inequality.
. Any value of y in this highlighted region, including -1, is going to satisfy the inequality.

EXAMPLE
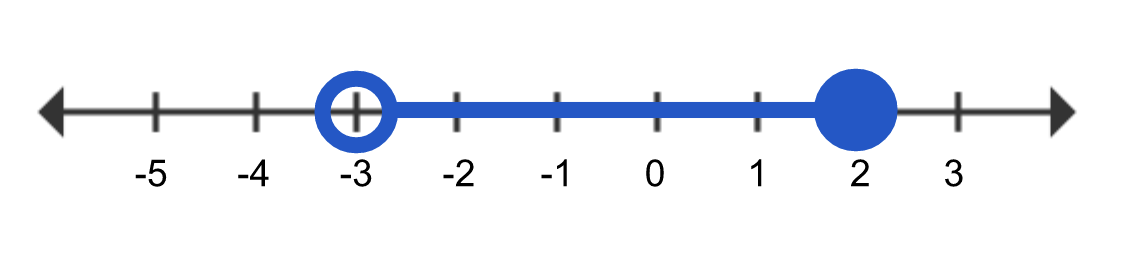
Graph the inequality .
.
 , the values for x that are going to satisfy this inequality have to be bigger than -3 and less than or equal to 2. We start by putting an open circle at -3 because we see that x cannot be exactly equal to -3. Then we are going to use a closed circle at 2 because we know that x can be equal exactly to 2.
, the values for x that are going to satisfy this inequality have to be bigger than -3 and less than or equal to 2. We start by putting an open circle at -3 because we see that x cannot be exactly equal to -3. Then we are going to use a closed circle at 2 because we know that x can be equal exactly to 2.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License