1. Rationalizing the Denominator

It is considered bad practice to have a radical in the denominator of a fraction. When this happens we multiply the numerator and denominator by the same thing in order to clear the radical. In the lesson on dividing radicals we talked about how this was done with monomials. Here we will look at how this is done with binomials.

If the binomial is in the numerator the process to rationalize the denominator is essentially the same as with monomials The only difference is we will have to distribute in the numerator.

hint

It is important to remember that when reducing the fraction we cannot reduce with just the 3 and 12 or just the 9 and 12. When we have addition or subtraction in the numerator or denominator we must divide all terms by the same number. As we are rationalizing it will always be important to constantly check our problem to see if it can be simplified more. We ask ourselves, can the fraction be reduced? Can the radicals be simplified? These steps may happen several times on our way to the solution.

If the binomial occurs in the denominator we will have to use a different strategy to clear the radical. Consider , if we were to multiply the denominator by 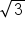we would have to distribute it and we would end up with . We have not cleared the radical, only moved it to another part of the denominator. So our current method will not work. Instead we will use what is called a conjugate. A conjugate is made up of the same terms, with the opposite sign in the middle. So for our example with in the denominator, the conjugate would be

term to know

Conjugate

The conjugate of a binomial is a binomial with the opposite sign between its terms.

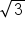The advantage of a conjugate is when we multiply them together we have , which is a difference and a sum. We know when we multiply these, we get a difference of squares. Squaring and 5, with subtraction in the middle gives the product:

Our answer when multiplying conjugates will no longer have a square root, which is exactly what we want.

big idea

To rationalize a denominator containing a radical expression, multiply the fraction using its conjugate. The product will no longer contain a radical.

EXAMPLE

In the previous example, we could have reduced by dividing by -2 instead of 2, giving . Both answers are correct.

EXAMPLE

The same process can be used when there is a binomial in the numerator and denominator. We just need to remember to FOIL out the numerator.

EXAMPLE

EXAMPLE

did you know

During the 5th century BC in India, Aryabhata published a treatise on astronomy. His work included a method for finding the square root of numbers that have many digits.