Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Solving an Exponential Equation

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to solve an exponential equation by rewriting the base. Specifically, this lesson will cover:

Table of Contents

1. Solving an Exponential Equation

When solving for any type of equation, a sound strategy is to apply inverse operations to undo operations being performed to the variable. Doing so isolates the variable to one side of the equation, where we can then evaluate the other side to find our solution.

In general, exponential equations can be solved by applying a logarithm to both sides of the equation. This is because logarithms and exponents are inverse operations. However, we will explore this method later in a different lesson. In this lesson, we focus on how to analyze the bases involved in the equations. If the bases are the same, or if they can be rewritten to match, we can actually solve exponential equations without using logarithms.

2. Exponential Equations with the Same Base

If the bases are the same in exponential equations, we can set the exponents equal to each other, and isolate the variable as we normally do with other equations.

EXAMPLE

Solve for x in the equation 6 to the power of 2 x plus 9 end exponent equals 6 to the power of short dash 5 plus 2 end exponent.

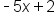In both exponential expressions, the base is 6. This means that the quantity of the exponent for 6 is the same on both sides of the equation, therefore 2 x plus 9 and short dash 5 x plus 2 must be equal quantities. We can create an equivalent equation that is actually linear in nature, and solve for x:

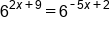
6 to the power of 2 x plus 9 end exponent equals 6 to the power of short dash 5 x plus 2 end exponent Set exponents equal to each other
2 x plus 9 equals short dash 5 x plus 2 Add 5x to both sides
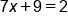
7 x plus 9 equals 2 Subtract 9 from both sides
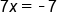
7 x equals short dash 7 Divide both sides by 7
x equals short dash 1 Our solution

3. Rewriting the Base

When we are working with exponential equations in which the base numbers are not the same, it may appear as though we cannot solve using the strategy described in the section above. However, by closely examining the base numbers, we may be able to rewrite one or more of the bases in order to create an equivalent equation with common bases. If we can do this, we can solve the equation using a similar strategy as before.

hint
When we use this strategy, we will need to apply the Power of a Power Property of Exponents. This property allows us to multiply exponents in cases where a base number is raised to an exponent power and then raised to an exponent power again.

formula to know
Power of a Power Property of Exponents
open parentheses a to the power of n close parentheses to the power of m equals a to the power of n m end exponent

EXAMPLE

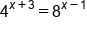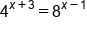
Solve for x in the equation 4 to the power of x plus 3 end exponent equals 8 to the power of x minus 1 end exponent.

At first glance, it may appear as though we cannot solve this equation using our strategy from before. However, we notice that both 4 and 8 are powers of 2. That is, 4 is the same as 2 squared and 8 is the same as 2 cubed. Let's make these substitutions in our equation by rewriting each base.

4 to the power of x plus 3 end exponent equals 8 to the power of x minus 1 end exponent Rewrite with same base of 2
open parentheses 2 squared close parentheses to the power of x plus 3 end exponent equals open parentheses 2 cubed close parentheses to the power of x minus 1 end exponent Equivalent equation

We can now multiply the two exponents on each side of the equation using the Power of Powers Property of Exponents and then solve as we did in the first example.

open parentheses 2 squared close parentheses to the power of x plus 3 end exponent equals open parentheses 2 cubed close parentheses to the power of x minus 1 end exponent Use Power of Powers Property and multiply exponents
2 to the power of 2 x plus 6 end exponent equals 2 to the power of 3 x minus 3 end exponent Set exponents equal to each other
2 x plus 6 equals 3 x minus 3 Add 3 to both sides
2 x plus 9 equals 3 x Subtract 2x from both sides
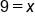
9 equals x Our solution

When x equals 9, the two sides of the equation are equal. We can test this by plugging 9 in for x back into the original equation.

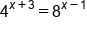
4 to the power of x plus 3 end exponent equals 8 to the power of x minus 1 end exponent Plug in 9 for x
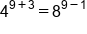
4 to the power of 9 plus 3 end exponent equals 8 to the power of 9 minus 1 end exponent Evaluate operations in exponents
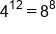
4 to the power of 12 equals 8 to the power of 8 Evaluate result using calculator
16 comma 777 comma 216 equals 16 comma 777 comma 216 This is a true statement

summary
There are two methods for solving exponential equations. For exponential equations with the same base, then simply solve by setting the exponents equal to each other. If the bases are not the same, then you will need to rewrite the base and use properties of exponents to obtain an equation with common bases. Then, write and solve an equation using just the expressions in the exponents.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Power of a Power Property of Exponents

open parentheses a to the power of n close parentheses to the power of m equals a to the power of n m end exponent

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.