Solving Exponential Equations using Logarithms

1. Exponential-Logarithmic Relationships

Exponential equations can be equivalently written using a logarithm. In general, we can say that the follow two equations are equivalent:

Exponential Equation	Logarithmic Equation

Notice that the base of the exponential expression becomes the base of the logarithmic expression. Also notice that y, which was the output of the exponential equation, is the input of the logarithmic operation. This is characteristic of inverse relationships.

When solving exponential equations using logarithms, we often apply two important properties of logarithms: the power property of logs and the change of base property of logs:

formula to know

Power Property of Logs

Change of Base Property of Logs

We most often use the change of base property when we wish to use our calculators to evaluate logs. This is because most calculators can only evaluate logs in base 10 (the common log) or e (the natural log).

2. Writing Exponential Equations as Logarithms

EXAMPLE

Solve the exponential equation .

One strategy for solving this equation is to see if 10.556 is a power of 4. If so, it is relatively easy to solve for x mentally, as x will be an integer, such as 1, 2, 3, and so on. However, there is no integer exponent we can apply to 4 to get a value of 10.556. In this case, it is helpful to write this into an equivalent logarithmic equation:

	Rewrite using a logarithmic eqution
	Equivalent equation to

Now that we have a logarithmic expression for x, we can use the change of base property to evaluate the log using our calculator:

	Apply the Change of Base Property of Logs
	Use calculator to evaluate
	Our solution

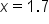
3. Applying Logarithms to Both Sides of an Equation

As with all equations, we can apply inverse operations to both sides of the equation in order to isolate the variable. The inverse operation of an exponent is the logarithm. In this next example, we will see how we can apply the logarithm and other inverse operations to isolate the variable.

EXAMPLE

Solve the exponential equation .

	Divide by 2 to have only on the left side
	Apply log of both sides
	Apply the Power Property of Logs
	Divide both sides by
	Use calculator to evaluate
	Our solution

big idea

When applying the log to both sides of an exponential equation, this enables us to apply the power property of logarithms. We can move the variable outside of the logarithm, as a scalar multiplier to the log. Then, we are able to isolate the variable by dividing everything else out.