Table of Contents |
An equation is a mathematical statement that expressions or quantities have the same value.
EXAMPLE
The equation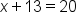 is saying that the quantity x plus 13 has the same value as 20.
is saying that the quantity x plus 13 has the same value as 20.
In the example above, we have a variable x. A variable is a value that can change. But when it is in an equation, there is then a certain value that makes the statement true. Sometimes, x could have several values that make it true. However, it is not always the case that x can be whatever it wants to be. It has to fit that particular equation.
Equations can also be written in the other direction and is known as the rule of symmetry.
EXAMPLE
In the previous example, we could say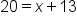 .
.
Solving linear equations is an important and fundamental skill in algebra. In algebra, we are often presented with a problem where the answer is known, but part of the problem is missing. The missing part of the problem is what we seek to find.
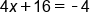
EXAMPLE
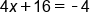
|
Replace x with -5 |
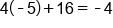
|
Multiply 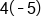
|

|
Add 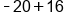
|
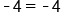
|
True! |
Now the equation comes out to a true statement! Notice also that if another number, for instance, 3, was plugged in, we would not get a true statement.
EXAMPLE
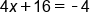
|
Replace x with 3 |
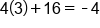
|
Multiply 
|
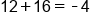
|
Add 
|
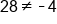
|
False! |
Due to the fact that this is not a true statement, this demonstrates that 3 is not the solution. However, depending on the complexity of the problem, this “guess and check” method is not very efficient. Thus, we take a more algebraic approach to solving equations. Here we will focus on what are called “one-step equations” or equations that only require one step to solve. While these equations often seem very fundamental, it is important to master the pattern for solving these problems so we can solve more complex problems.
To solve equations, the general rule is to do the opposite. For addition problems, this means that we will do the opposite operation, which is subtraction.
EXAMPLE
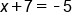
|
The 7 is added to the x, so subtract 7 from both sides |
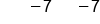
|
The 7's on the left side cancel, leaving x. Subtract 7 from -5 |
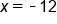
|
Our Solution |
The same process is used in each of the following examples.
EXAMPLE
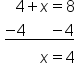
|
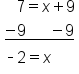
|
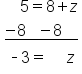
|
In a subtraction problem, we get rid of negative numbers by adding them to both sides of the equation.
EXAMPLE

|
The 5 is subtracted from x, so add 5 to both sides |

|
The 5's on the left side cancel, leaving x. Add 4 and 5 together |

|
Our Solution |
The same process is used in each of the following examples. Notice that each time we are getting rid of a negative number by adding.
EXAMPLE

|
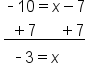
|
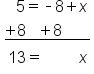
|
With a multiplication problem, we get rid of the number by dividing both sides. Note that we are showing division with a fraction bar, for instance,  . Using a fraction bar is the same as division.
. Using a fraction bar is the same as division.  is the same as
is the same as  .
.
EXAMPLE
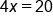
|
Variable is multiplied by 4, so divide both sides by 4 |
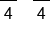
|
The 4's on the left side cancel, leaving x. Divide 20 by 4 |

|
Our Solution |
With multiplication problems, it is very important that care is taken with signs. If x is multiplied by a negative then we will divide by a negative.
EXAMPLE

|
Variable is multiplied by -5, so divide both sides by -5 |
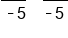
|
The -5's on the left side cancel, leaving x. Divide 30 by -5 |
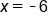
|
Our Solution |
The same process is used in each of the following examples. Notice how negative and positive numbers are handled as each problem is solved.
EXAMPLE
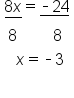
|

|
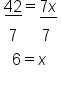
|
In division problems, we get rid of the denominator by multiplying on both sides.
EXAMPLE
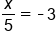
|
Variable is divided by  , so multiply both sides by 5 , so multiply both sides by 5
|

|
The 5's on the left side cancel, leaving x. Multiply -3 and 5 |
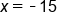
|
Our Solution |
The same process is used in each of the following examples.
EXAMPLE
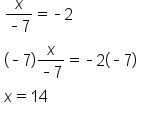
|
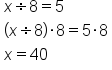
|
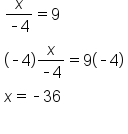
|
The process described above is fundamental to solving equations. Once this process is mastered, the problems we will see have several more steps. These problems may seem more complex, but the process and patterns used will remain the same.
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License