Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Solving Single-Step Equations

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to identify the operation needed to solve a single-step equation. Specifically, this lesson will cover:

Table of Contents

1. Equations

An equation is a mathematical statement that expressions or quantities have the same value.

EXAMPLE

The equation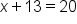 x plus 13 equals 20 is saying that the quantity x plus 13 has the same value as 20.

In the example above, we have a variable x. A variable is a value that can change. But when it is in an equation, there is then a certain value that makes the statement true. Sometimes, x could have several values that make it true. However, it is not always the case that x can be whatever it wants to be. It has to fit that particular equation.

Equations can also be written in the other direction and is known as the rule of symmetry.

EXAMPLE

In the previous example, we could say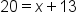 20 equals x plus 13.

term to know
Equation
A mathematical statement that two quantities or expressions are equal in value.

2. Solving Single-Step Equations

Solving linear equations is an important and fundamental skill in algebra. In algebra, we are often presented with a problem where the answer is known, but part of the problem is missing. The missing part of the problem is what we seek to find.

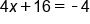
4 x plus 16 equals short dash 4

Notice the above problem has a missing part, or unknown, that is marked by x. If we are given that the solution to this equation is -5, it could be plugged into the equation, replacing the x with -5. This is shown below:

EXAMPLE

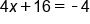
4 x plus 16 equals short dash 4 Replace x with -5
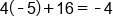
4 open parentheses short dash 5 close parentheses plus 16 equals short dash 4 Multiply 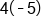4 open parentheses short dash 5 close parentheses
short dash 20 plus 16 equals short dash 4 Add 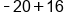short dash 20 plus 16
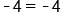
short dash 4 equals short dash 4 True!

Now the equation comes out to a true statement! Notice also that if another number, for instance, 3, was plugged in, we would not get a true statement.

EXAMPLE

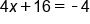
4 x plus 16 equals short dash 4 Replace x with 3
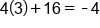
4 open parentheses 3 close parentheses plus 16 equals short dash 4 Multiply 4 open parentheses 3 close parentheses
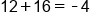
12 plus 16 equals short dash 4 Add 12 plus 16
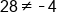
28 not equal to short dash 4 False!

Due to the fact that this is not a true statement, this demonstrates that 3 is not the solution. However, depending on the complexity of the problem, this “guess and check” method is not very efficient. Thus, we take a more algebraic approach to solving equations. Here we will focus on what are called “one-step equations” or equations that only require one step to solve. While these equations often seem very fundamental, it is important to master the pattern for solving these problems so we can solve more complex problems.

2a. Addition Problems

To solve equations, the general rule is to do the opposite. For addition problems, this means that we will do the opposite operation, which is subtraction.

EXAMPLE

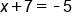
x plus 7 equals short dash 5 The 7 is added to the x, so subtract 7 from both sides
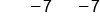
space space space space space space space minus 7 space space space space space space minus 7 The 7's on the left side cancel, leaving x. Subtract 7 from -5
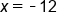
x equals short dash 12 Our Solution

The same process is used in each of the following examples.

EXAMPLE

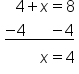
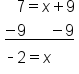
table attributes columnalign left end attributes row cell space space space 4 plus x equals 8 end cell row cell stack negative 4 space space space space space space minus 4 with bar below end cell row cell space space space space space space space space space x equals 4 end cell end table table attributes columnalign left end attributes row cell space space space 7 equals x plus 9 end cell row cell stack negative 9 space space space space space space minus 9 with bar below end cell row cell short dash 2 equals x end cell end table 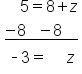table attributes columnalign left end attributes row cell space space space space 5 equals 8 plus z end cell row cell stack negative 8 space space space minus 8 space space space space with bar below end cell row cell space short dash 3 equals space space space space space z end cell end table

hint
Notice that when we subtracted 7 from the left side to cancel this value, we also had to subtract 7 from the right side. This is referred to as the rule of equality. This is true for any operation; if you perform an operation on one side of the equation, you must do the same operation on the other side.

term to know
Rule of Equality
Any operation performed on one side of the equation must be performed on the other side, in order to keep quantities equal in value.

2b. Subtraction Problems

In a subtraction problem, we get rid of negative numbers by adding them to both sides of the equation.

EXAMPLE

x minus 5 equals 4 The 5 is subtracted from x, so add 5 to both sides
stack space space plus 5 space space plus 5 with bar below The 5's on the left side cancel, leaving x. Add 4 and 5 together
x equals 9 Our Solution

The same process is used in each of the following examples. Notice that each time we are getting rid of a negative number by adding.

EXAMPLE

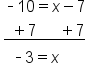
table attributes columnalign left end attributes row cell short dash 6 plus x equals short dash 2 end cell row cell stack plus 6 space space space space space space space space space plus 6 with bar below end cell row cell space space space space space space space space space x equals 4 end cell end table table attributes columnalign left end attributes row cell short dash 10 equals x minus 7 end cell row cell stack space space plus 7 space space space space space space plus 7 with bar below end cell row cell space space short dash 3 equals x end cell end table 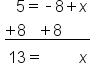table attributes columnalign left end attributes row cell space space space 5 equals short dash 8 plus x end cell row cell stack plus 8 space space space plus 8 space space space space space space space with bar below end cell row cell space 13 equals space space space space space space space space space x end cell end table

2c. Multiplication Problems

With a multiplication problem, we get rid of the number by dividing both sides. Note that we are showing division with a fraction bar, for instance, 24 over 6 equals 4. Using a fraction bar is the same as division. 15 over 3 equals 5 is the same as 15 divided by 3 equals 5.

EXAMPLE

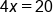
4 x equals 20 Variable is multiplied by 4, so divide both sides by 4
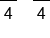
stack space 4 space with bar on top space space space space stack space 4 space with bar on top The 4's on the left side cancel, leaving x. Divide 20 by 4
x equals 5 Our Solution

With multiplication problems, it is very important that care is taken with signs. If x is multiplied by a negative then we will divide by a negative.

EXAMPLE

short dash 5 x equals 30 Variable is multiplied by -5, so divide both sides by -5
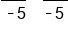
stack space short dash 5 with bar on top space space space space stack short dash 5 space with bar on top The -5's on the left side cancel, leaving x. Divide 30 by -5
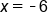
x equals short dash 6 Our Solution

The same process is used in each of the following examples. Notice how negative and positive numbers are handled as each problem is solved.

EXAMPLE

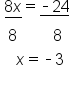
table attributes columnalign left end attributes row cell stack 8 x with bar below equals stack short dash 24 with bar below end cell row cell space 8 space space space space space space space space space 8 end cell row cell space space space x equals short dash 3 end cell row blank end table table attributes columnalign left end attributes row cell stack short dash 4 x with bar below equals stack short dash 20 with bar below end cell row cell space short dash 4 space space space space space space space short dash 4 end cell row cell space space space space space space x equals 5 end cell row blank end table 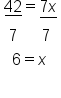table attributes columnalign left end attributes row cell 42 with bar below equals stack 7 x with bar below end cell row cell space 7 space space space space space space 7 end cell row cell space space 6 equals x end cell row blank end table

2d. Division Problems

In division problems, we get rid of the denominator by multiplying on both sides.

EXAMPLE

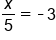
x over 5 equals short dash 3 Variable is divided by 5, so multiply both sides by 5
open parentheses 5 close parentheses x over 5 equals short dash 3 open parentheses 5 close parentheses The 5's on the left side cancel, leaving x. Multiply -3 and 5
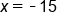
x equals short dash 15 Our Solution

The same process is used in each of the following examples.

EXAMPLE

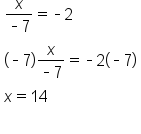
table attributes columnalign left end attributes row cell fraction numerator x over denominator short dash 7 end fraction equals short dash 2 end cell row cell open parentheses short dash 7 close parentheses fraction numerator begin display style x end style over denominator begin display style short dash 7 end style end fraction equals short dash 2 open parentheses short dash 7 close parentheses end cell row cell x equals 14 end cell row blank end table 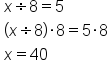table attributes columnalign left end attributes row cell x divided by 8 equals 5 end cell row cell open parentheses x divided by 8 close parentheses times 8 equals 5 times 8 end cell row cell x equals 40 end cell end table 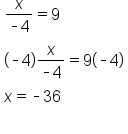table attributes columnalign left end attributes row cell fraction numerator x over denominator short dash 4 end fraction equals 9 end cell row cell open parentheses short dash 4 close parentheses fraction numerator begin display style x end style over denominator begin display style short dash 4 end style end fraction equals 9 open parentheses short dash 4 close parentheses end cell row cell x equals short dash 36 end cell row blank end table

The process described above is fundamental to solving equations. Once this process is mastered, the problems we will see have several more steps. These problems may seem more complex, but the process and patterns used will remain the same.

big idea
To solve single-step equations, first identify the operation being applied to the variable. To isolate the variable, apply the inverse operation. Addition and subtraction are inverses of each other; multiplication and division are inverses of each other.

summary
Solving single-step equations involves isolating the variable that you're trying to solve for by using an inverse operation. Any operation that you do on one side of the equation needs to be done on the other side. You can always check your solution by substituting it in for the variable in your original equation and seeing if the statement holds true. This is good practice to get into when you're doing simple equations because when you do things more complicated, it's more likely that you're going to be making a mistake.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Terms to Know
Equation

A mathematical statement that two quantities or expressions are equal in value.

Rule of Equality

Any operation performed on one side of the equation must be performed on the other side, in order to keep quantities equal in value.

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.