Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Sum of a Finite Geometric Sequence

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to find the sum of a finite geometric sequence. Specifically, this lesson will cover:

Table of Contents

1. Formula for the Sum of a Finite Geometric Sequence

Consider the following geometric sequence: 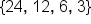left curly bracket 24 comma space 12 comma space 6 comma space 3 right curly bracket. To find the sum of this finite sequence, it is simple enough to concretely add together all of the terms:

24 plus 12 plus 6 plus 3 equals 45

However, there is a useful formula we can use in cases where this may be difficult to do, for example, if there were 100 terms to add.

formula to know
Sum of a Finite Geometric Sequence
S subscript n equals a subscript 1 times left parenthesis fraction numerator 1 minus r to the power of n over denominator 1 minus r end fraction right parenthesis

In this formula:

  • S subscript n is the sum of n terms
  • a subscript 1 is the value of the first term
  • r is the common ratio
  • n is the number of terms

EXAMPLE

Using the geometric sequence above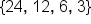 left curly bracket 24 comma space 12 comma space 6 comma space 3 right curly bracket, confirm that the sum of the four terms above is 45 by using the formula as well.

Let's identify a subscript 1, r, and n:
  • a subscript 1: The first term is 24.
  • r: The common ratio can be found by dividing any two consecutive numbers: 12 divided by 24 equals 0.5.
  • n: There are 4 terms, so n is 4.
Plug these values into the Sum of a Finite Geometric Sequnce formula:

S subscript n equals a subscript 1 times open parentheses fraction numerator 1 minus r to the power of n over denominator 1 minus r end fraction close parentheses Plug in n equals 4 comma space a subscript 1 equals 24 comma space r equals 0.5
S subscript 4 equals 24 times open parentheses fraction numerator 1 minus 0.5 to the power of 4 over denominator 1 minus 0.5 end fraction close parentheses Evaluate the exponent
S subscript 4 equals 24 times open parentheses fraction numerator 1 minus 0.0625 over denominator 1 minus 0.5 end fraction close parentheses Simplify the numerator and denominator
S subscript 4 equals 24 times open parentheses fraction numerator 0.9375 over denominator 0.5 end fraction close parentheses Evaluate the fraction
S subscript 4 equals 24 times open parentheses 1.875 close parentheses Multiply
S subscript 4 equals 45 Our solution

2. Geometric Sums when r is Greater than 1

Our formula works for any value of r, although when we are working through the calculations, it may seem as though something must be off. Don't worry, as long as you follow the steps properly, you should arrive at the correct sum.

EXAMPLE

Find the sum of the geometric sequence left curly bracket 32 comma space 48 comma space 72 comma space 108 comma space 162 right curly bracket.

Again, let's identify a subscript 1, r, and n:
  • a subscript 1: The value of the first term is 32.
  • r: The common ratio is 1.5, which is found by dividing any two consecutive terms, such as 108 divided by 72 equals 1.5.
  • n: Since we have 5 terms in the sequence, n equals 5.
Applying the formula, we can find the sum of these 5 terms:

S subscript n equals a subscript 1 times open parentheses fraction numerator 1 minus r to the power of n over denominator 1 minus r end fraction close parentheses Plug in n equals 5 comma space a subscript 1 equals 32 comma space r equals 1.5
S subscript 5 equals 32 times open parentheses fraction numerator 1 minus 1.5 to the power of 5 over denominator 1 minus 1.5 end fraction close parentheses Evaluate the exponent
S subscript 5 equals 32 times open parentheses fraction numerator 1 minus 7.59375 over denominator 1 minus 1.5 end fraction close parentheses Simplify the numerator and denominator
S subscript 5 equals 32 times open parentheses fraction numerator short dash 6.59375 over denominator short dash 0.5 end fraction close parentheses Evaluate the fraction
S subscript 5 equals 32 times open parentheses 13.1875 close parentheses Multiply
S subscript 5 equals 422 Our solution

Checking concretely: 32 plus 48 plus 72 plus 108 plus 162 equals 422

3. Geometric Sums when r is Less than 0

The formula even works if the common ratio is a negative number.

EXAMPLE

Find the sum of the geometric sequence left curly bracket 6 comma space short dash 18 comma space 54 comma space short dash 162 comma space 486 right curly bracket.

First, identify a subscript 1, r, and n:
  • a subscript 1: The first term is 6
  • r: Here, the common ratio is -3, because we multiply 6 by -3 to get -18, -18 by -3 to get 54, and so on.
  • n: There are 5 terms so n equals 5
To find the sum of these 5 terms using the formula, we take the following steps:

S subscript n equals a subscript 1 times open parentheses fraction numerator 1 minus r to the power of n over denominator 1 minus r end fraction close parentheses Plug in n equals 5 comma space a subscript 1 equals 6 comma space r equals short dash 3
S subscript 5 equals 6 times open parentheses fraction numerator 1 minus open parentheses short dash 3 close parentheses to the power of 5 over denominator 1 minus open parentheses short dash 3 close parentheses end fraction close parentheses Evaluate the exponent
S subscript 5 equals 6 times open parentheses fraction numerator 1 minus open parentheses short dash 243 close parentheses over denominator 1 minus open parentheses short dash 3 close parentheses end fraction close parentheses Simplify the numerator and denominator
S subscript 5 equals 6 times open parentheses 244 over 4 close parentheses Evaluate the fraction
S subscript 5 equals 6 times open parentheses 61 close parentheses Multiply
S subscript 5 equals 366 Our solution

Confirming concretely: 6 minus 18 plus 54 minus 162 plus 486 equals 366

4. Partial Sums

We can even use the formula to find a partial sum of a geometric sequence. A partial sum means that we add some of the terms in the sequence, but not all of them.

EXAMPLE

Find the sum of the terms 3 through 8 in the geometric sequence with 12 terms:

left curly bracket 13 comma space 26 comma space 52 comma space 104 comma space 208 comma space 416 comma space 832 comma space 1664 comma space 3328 comma space 6656 comma space 13312 comma space 26624 right curly bracket

If we want to find the sum of terms 3 through 8, we would make the following adjustments to our formula:
  • a subscript 1: We will consider a subscript 1 to be 52. Although it is the 3rd term in the sequence, it is the 1st term we wish to include in the sum.
  • r: The common ratio is 2, since 26 divided by 13 equals 2
  • n: We will use n equals 6 because the sum of terms 3 through 8 consists of 6 terms altogether: 3rd term, 4th term, 5th term, 6th term, 7th term, and 8th term.
Everything else about the formula remains the same:

S subscript n equals a subscript 1 times open parentheses fraction numerator 1 minus r to the power of n over denominator 1 minus r end fraction close parentheses Plug in n equals 6 comma space a subscript 1 equals 52 comma space r equals 2
S subscript 6 equals 52 times open parentheses fraction numerator 1 minus 2 to the power of 6 over denominator 1 minus 2 end fraction close parentheses Evaluate the exponent
S subscript 6 equals 52 times open parentheses fraction numerator 1 minus 64 over denominator 1 minus 2 end fraction close parentheses Simplify the numerator and denominator
S subscript 6 equals 52 times open parentheses fraction numerator short dash 63 over denominator short dash 1 end fraction close parentheses Evaluate the fraction
S subscript 6 equals 52 times open parentheses 63 close parentheses Multiply
S subscript 6 equals 3276 Our solution

Adding concretely: 52 plus 104 plus 208 plus 416 plus 832 plus 1664 equals 3276

summary
In the formula for the sum of a finite geometric sequence, a subscript 1 is the first term in the sequence, r is the common ratio between consecutive terms, and n is the number of terms. The formula for finding the sum of a finite geometric sequence can be used when r is both positive and negative, or the geometric sum when r is greater than 1 or r is less than 0. The formula can also be used to calculate a partial sum of a finite or infinite sequence.

Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Sum of a Finite Geometric Sequence

S subscript n equals a subscript 1 times open parentheses fraction numerator 1 minus r to the power of n over denominator 1 minus r end fraction close parentheses

© 2024 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.