Table of Contents |
Polynomial long division sounds like a complicated process, and it can be without an understanding of the similarities between the long division from your elementary school days. The process, or algorithm - the steps we take to arrive at our solution - is the same, we are just dealing with more complicated terms.
EXAMPLE
Divide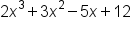 by
by  .
.
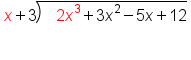
|
Divide 
|
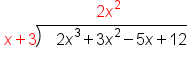
|
Multiply 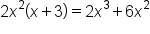
|

|
Subtract 
|

|
Bring down next term, -5x |
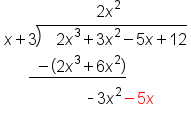
|
Repeat process |

|
Divide 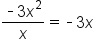
|
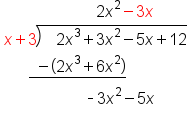
|
Multiply 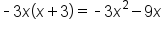
|
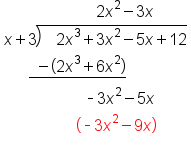
|
Subtract 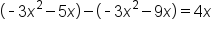
|
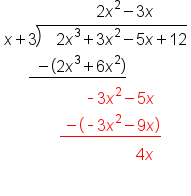
|
Bring down next term, +12 |
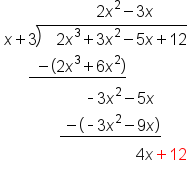
|
Repeat process |
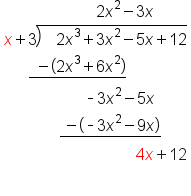
|
Divide 
|

|
Multiply 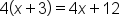
|
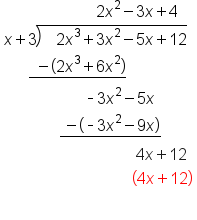
|
Subtract 
|

|
Our solution with 0 Remainder |
 with zero remainder.
with zero remainder.
Synthetic division is a process that is designed to be easier than polynomial long division. It works primarily with the coefficients to the term, and simplifies the steps in the algorithm to arrive at the same solution.
We are going to do the same division example as above, but set the problem up using synthetic division:
EXAMPLE
Divide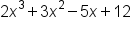 by
by  .
.

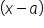 form for the divisor (what we are dividing by). Because we generally say
form for the divisor (what we are dividing by). Because we generally say 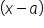 , if the factor we are dividing by has a plus sign, the value of "a" is actually negative. Since we are dividing by x + 3, then our divisor is actually -3.
, if the factor we are dividing by has a plus sign, the value of "a" is actually negative. Since we are dividing by x + 3, then our divisor is actually -3.


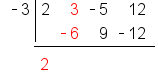

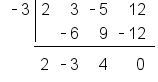
 .
.
 with a remainder of zero, which is exactly what we got using the long division process in the section above.
with a remainder of zero, which is exactly what we got using the long division process in the section above.
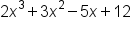 had a degree of 3. So the quotient will have a degree of 2, and we can use this to create our solution
had a degree of 3. So the quotient will have a degree of 2, and we can use this to create our solution  .
.
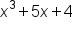 has no
has no  term, so the box would look like:
term, so the box would look like:

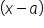 as the denominator. For example, let's say we worked through the synthetic division, and our last number was a -2, instead of 0. We would write our solution as:
as the denominator. For example, let's say we worked through the synthetic division, and our last number was a -2, instead of 0. We would write our solution as:
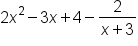
Source: ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE, AN OPEN SOURCE TEXTBOOK AVAILABLE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License