Time Value of Money Calculations

1. TVM: Plan with Confidence

During your lifetime financial journey, you will be faced with many unique financial opportunities to invest, borrow, and plan for the future. Knowing how much you can afford to borrow before you apply for a loan or talk with a lender is a powerful tool. Additionally, having the ability to determine your loan payment based on the amount borrowed and interest rate charged might just protect you from being overcharged by thousands of dollars. Finally, calculating how much you should be saving for long-term goals will give you confidence in your plans or the opportunity to be agile and adjust your plans while you still have time to make changes.

In this topic, you’ll learn how to perform your own time value of money (TVM) calculations, which is an essential tool for building a strong financial future.

2. Solving TVM Problems

There are multiple ways to solve TVM problems. Most often people prefer to use a spreadsheet program like Microsoft® Excel or Google® Sheets, a financial calculator, or an app designed to solve these types of problems. These tools can help improve your productivity and they can make it easier to adjust plans when needed. However, there is value in learning how to do TVM calculations yourself either using formulas or compound interest tables. We will provide some basic steps to follow when using a calculator to solve TVM problems. However, you should consult the user manual specific to your calculator for more detailed instructions.

hint

When you see the term "annuity due," remember that the payments or deposits come at the beginning of the period. The annuity due formula accounts for this by inflating the traditional result for the calculation’s rate of return. All of the other formulas use end-of-period assumptions.

2a. Future Value of a Lump Sum

Here’s an example showing how to calculate a future value.

EXAMPLE

Let’s say that you receive $1,000 at your college graduation. If you invest the gift and earn 8% annually, how much will you have in 20 years? Let’s first solve using the following formula.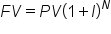

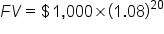
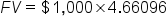
Next, let’s solve the problem using a TVM table. The table below shows the Future Value of $1 table that you’ll need to use. Here’s how to use the table.

step by step

1. Find the number of periods (20) in the first column.
2. Move to the right until you find the future value factor that corresponds to the 8% column: 4.66096.
3. Multiply the factor by your present value ($1,000): $1,000 x 4.6609, or $4,660.96.

You should notice two things. First, the solution is the same whether calculated with the formula or the table. Second, the future value factor in the table (4.66096) is basically the same as 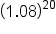in the formula.

Table: Future Value of $1

2b. Present Value of a Lump Sum

Imagine you are offered the choice of taking $1,000 today or $1,200 in 5 years. Before you can make a decision, you also need to know what rate of return you can earn on your savings (sometimes called the discount rate). You determine that you can earn 5%. What should you do? You should use the present value of a lump sum formula to compare the $1,000 that you can receive today to the present value of $1,200 as follows:

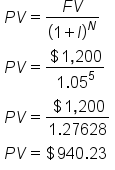
As you can see, the present value of receiving $1,200 in 5 years is only $940.22. So, it’s better to take the $1,000 right now.

The table below shows the Present Value of $1 table that you can also use to solve the problem.

hint

Note that the Present Value of $1 table is set up exactly the same as the Future Value of $1 table.

Table: Present Value of $1

step by step

1. Find the number of periods in column 1, which is 5.
2. Go to the right until you find the present value factor in the 5% column: 0.78353.
3. Multiply $1,200 by 0.78353 and you will get $940.24 (which is very close to the formula calculation).

term to know

Discount Rate

Rate of return you can earn on your savings.

2c. Future Value of an Annuity

By now, you might be asking how you can determine how much money you’ll have in the future if you save money every year instead of starting with a lump sum. When you start saving money on a regular basis, this is called an annuity. In TVM lingo, the amount saved or paid each period is referred to as a payment (PMT). Payments are different than present or future values because, as the name implies, a payment happens more than once.

EXAMPLE

How much, for example, will you accumulate in 20 years if you start saving $1,000 every year (each payment is the same amount) and earn 9% on your savings? The following formula can be used to answer this question: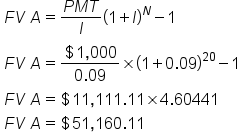

step by step

1. Just like the other table examples, start by finding the number of payments (20) in the first column.
2. Go to the right until you find the future value factor corresponding to the 9% column: 51.16012.
3. Multiply $1,000 by 51.16012. This gives you a future value of $51,160.12, which is nearly the same as what you estimated using the formula.

Table: Future Value of Annuity for $1 at the End of Each Period

think about it

The present value of an annuity is another TVM calculation that’s useful when planning your finances. What do you think are similarities and differences between the calculations for the present value of an annuity and the present value of a lump sum?

Note: calculations for present value of an annuity are beyond the scope of this tutorial.

2d. Payments

There are times you’ll need to calculate what is called an amortized payment – a payment of the same amount for a set number of months or years – such as for a car loan or mortgage. To do so, you should use the following formula:

formula to know

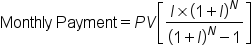
In the formula, PV is the amount borrowed, I = interest rate, and N = number of payments.

EXAMPLE

For example, say that Max wants to borrow $250,000 to purchase a home. He can get a 30-year loan at a 6% interest rate. To help Max determine if he can afford this loan, you first need to convert the years to months and the yearly rate of interest to monthly interest because Max will be making monthly payments.

• 
• 

You can now use the following formula to determine how much Max’s monthly payment will be (that is, you can calculate his principal and interest payment).



If you round the answer, Max will need to pay approximately $1,500 per month for the next 30 years to pay off the home mortgage loan.

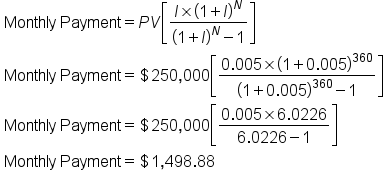
You can also solve this problem using an amortization schedule. The factors shown in the table below show the monthly dollar payment needed to pay off a $1,000 loan.

Table: Amortization Schedule for Monthly Payments for Every $1,000 Borrowed

Years	5	10	15	20	25	30
3.00%	$17.97	$9.66	$6.91	$5.55	$4.74	$4.22
3.50%	$16.67	$8.33	$5.56	$4.17	$3.33	$2.78
4.00%	$18.42	$10.12	$7.40	$6.06	$5.28	$4.77
4.50%	$18.64	$10.36	$7.65	$6.33	$5.56	$5.07
5.00%	$18.87	$10.61	$7.91	$6.60	$5.85	$5.37
5.50%	$19.10	$10.85	$ 8.17	$6.88	$6.14	$5.68
6.00%	$19.33	$11.10	$8.44	$7.16	$6.44	$6.00
6.50%	$19.57	$11.35	$8.71	$7.46	$6.75	$6.32
7.00%	$19.80	$11.61	$8.99	$7.75	$7.07	$6.65
7.50%	$20.04	$11.87	$9.27	$8.06	$7.39	$6.99
8.00%	$20.28	$12.13	$9.56	$8.36	$7.72	$7.34
8.50%	$20.52	$12.40	$9.85	$8.68	$8.05	$7.69
9.00%	$20.76	$12.67	$10.14	$9.00	$8.39	$8.05
9.50%	$21.00	$12.94	$10.44	$9.32	$8.74	$8.41
10.00%	$21.25	$13.22	$10.75	$9.65	$9.09	$8.78

To estimate the monthly payment needed by Max:

step by step

1. Find the interest rate of the loan in the first column.
2. Go to the right until you find the amortization factor matching 30 years: $6.00 (Max will pay $6.00 for every $1,000 borrowed).
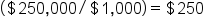3. Divide the loan amount by $1,000: (you need to do this to keep the factors consistent with the loan amount).
4. Multiply 250 by $6.00 to get $1,500, which is a very close approximation of the actual amount of the loan payment.

term to know

Amortized Payment

A payment of the same amount for a set number of months or years, such as for a car loan or mortgage.

Source: This content has been adapted from Chapter 2.3 of Introduction to Personal Finance: Beginning Your Financial Journey. Copyright © 2019 John Wiley & Sons, Inc. All rights reserved. Used by arrangement with John Wiley & Sons, Inc.

Wiley and the Wiley logo are trademarks or registered trademarks of John Wiley & Sons, Inc. and/or its affiliates in the United States and other countries.