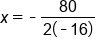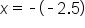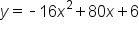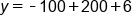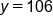EXAMPLE
Think about a volleyball being shot in the air in a vertical motion, once again going up, and eventually coming back down to the ground. This relationship can be shown with the following quadratic equation:
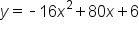
In this equation,
y equals the height of the ball, and
x is time. The graph below shows this relationship between the height of the ball in relationship to time:

We see that the x-axis represents time, measured in seconds, and the y-axis represents height, measured in feet.
The coefficients in this equation have important meanings within the context.
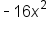
comes from the force of gravity on Earth, 80
x represents the velocity of the volleyball (in this case, it is 80 ft/s), and 6 represents the height of the volleyball player hitting the ball.
We can use this quadratic equation to answer questions about the maximum height that the ball will reach before it begins to come back down to the ground. Looking back at our graph, we notice that the maximum height of the volleyball is at the vertex of the parabola. How can we algebraically determine the coordinates of a vertex?
We use the following equation to find the x-coordinate of the vertex (which is also the equation to the axis of symmetry of the parabola):
-
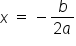 , where
, where  and b come from coefficients of the equation in standard form
and b come from coefficients of the equation in standard form
First, identify the coefficients

and
b in the original equation:
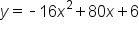
|
Identify coefficients  b, and c b, and c
|
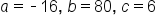
|
Plug into formula for x-coordinate of vertex
|
Now we can find the x-coordinate of the vertex.

|
Plug 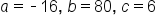 into formula into formula
|
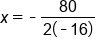
|
Evaluate denominator
|

|
Divide 80 by -32
|
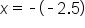
|
Simplify
|

|
x-coordinate of vertex
|
Our solved value for
x represents the time at which the ball will reach the maximum height. We would like to calculate the height. To do this, we must plug this value of
x back into the equation and find the associated y-value.
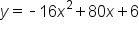
|
Plug 2.5 in for x
|

|
Evaluate
|
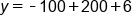
|
Simplify
|
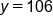
|
Our solution
|
This means that after 2.5 seconds, the volleyball will reach a maximum height of 106 feet.


 . Another method is to use the quadratic formula, which uses the coefficients of the equation in standard form (
. Another method is to use the quadratic formula, which uses the coefficients of the equation in standard form ( b, and c). We will use the quadratic formula to solve this equation, because by the looks of the coefficients in the equation, factoring is either going to be difficult or impossible.
b, and c). We will use the quadratic formula to solve this equation, because by the looks of the coefficients in the equation, factoring is either going to be difficult or impossible.
 b, and c:
b, and c:

 b, and c
b, and c

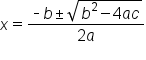
 into quadratic formula
into quadratic formula








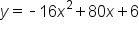

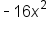 comes from the force of gravity on Earth, 80x represents the velocity of the volleyball (in this case, it is 80 ft/s), and 6 represents the height of the volleyball player hitting the ball.
comes from the force of gravity on Earth, 80x represents the velocity of the volleyball (in this case, it is 80 ft/s), and 6 represents the height of the volleyball player hitting the ball.
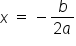 , where
, where  and b come from coefficients of the equation in standard form
and b come from coefficients of the equation in standard form and b in the original equation:
and b in the original equation:
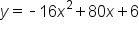
 b, and c
b, and c
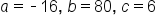

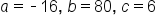 into formula
into formula